【 問 題 】

　半径 r の円の中心を点Oとし、円周上に点Sをとる。線分OS上に点Pをとり、線分PSの長さを a とする。点Pを通り線分OSに垂直な直線が円周と交わる点の一つを点Qとする。点Pを通り線分QOに垂直な直線が線分QOと交わる点を点Rとする。

　　　　　

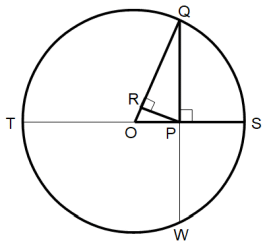
　　(１)　線分QP と 線分QR の長さを r と a を用いて表わせ。
　　(２)　相加平均 ≧ 相乗平均 ≧ 調和平均　であることを示せ。

【 解 答 】

（１）

線分QPの長さを x 、線分QRの長さを y とする。
方べきの定理より、 TP × PS ＝ WP × PQ
よって、 ( 2r−a ) × a ＝ x²
よって、
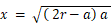
△QPR と △QOP は相似より 、QP : QR ＝ QO : QP
よって、 x : y ＝ r : x
よって、
　　　

（２）

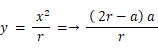
図より次の式が成り立つことが解る。
　　
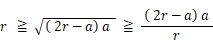
b ＝ 2r−a と置くと、
　　
　　
　　
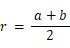
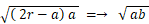
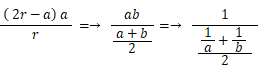
よって、
　　
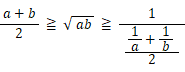
したがって、 相加平均 ≧ 相乗平均 ≧ 調和平均　であることが解った。

（３）

普通に　相加平均 ≧ 相乗平均 ≧ 調和平均　を証明してみよう。
　　
　　　　　　　　　
　　　　　　　　　
　　
　　　　　　　　　
　　　　　　　　　
　　　　　　　　　

【 参 考 】

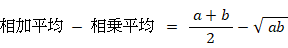
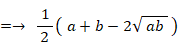
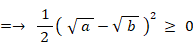
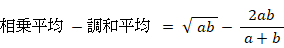
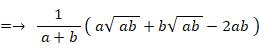
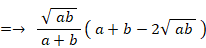
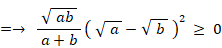
(１)　相乗平均を求める問題
　　　GNPは 昨年は 1.05倍、今年は 1.03倍 になった。この２年間のGNPの平均年間成長率は？

(２)　調和平均を求める問題
　　　行きは 40 km/時、帰りは 60 km/時 の速さであった。平均の速さは？