微小局所平面の公転は、微小局所平面の重心の移動形態の１つです。
　微小局所平面の自転は、微小局所平面の重心を通る軸を中心とする回転です。

　微小局所平面の重心を貫かない直線軸の回りの微小局所平面の回転は、公転です。公転半径は微小局所平面の重心の直線軸からの距離になります。その直線軸を「公転軸」と言うことにします。

　微小局所平面内が微小局所平面外を通る「公転軸」を中心に角速度 ω で公転しているときに、微小局所平面内のすべての点が同じ角速度 ω で公転している場合について、これから考察して参ります。

　公転している微小局所平面にはもう一つの回転中心直線軸が生じています。それは微小局所平面の重心を貫いて「公転軸」に平行な直線です。その回転中心直線軸を「自転軸」と言うことにします。微小局所平面の「自転軸」回りの回転は「自転」です。微小局所平面は「自転軸」を中心に角速度 ω で自転しています。
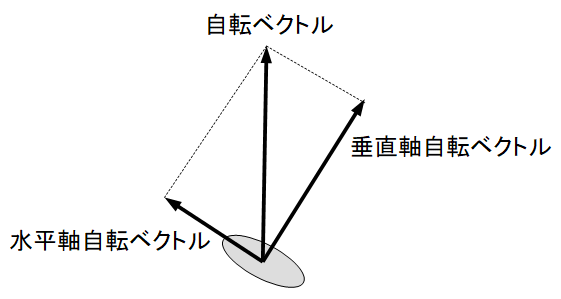
　「自転」は、２つの回転に分解することができます。それは、微小局所平面に垂直な方向 と「自転軸」の微小局所平面への投影方向 とにです。前者を「垂直軸自転（ ２次元的自転 ）の角速度」と言い、後者を「水平軸自転（ ３次元的自転 ）の角速度」と言うことにしましょう。次の式が成り立ちます。

　　自転の角速度の大きさの２乗
　　　　＝　垂直軸自転の角速度の大きさの２乗 ＋ 水平軸自転の角速度の大きさの２乗

　角速度 ω で回転しているレコード盤の上に描かれた微小局所平面は、角速度 ω で公転していると同時に、角速度 ω で垂直軸自転しています。ただし、水平軸自転はしていません。
　角速度 ω で回転しているレコード盤の上に垂直に立てられた微小局所平面は、角速度 ω で公転していると同時に、角速度 ω で水平軸自転しています。ただし、垂直軸自転はしていません。

　　　　　　　　　　　　　

　　　※ 参照：
　　　　　　 大学生のための物理学 ＞ 力学 ＞ フーコーの振り子（ 入門編 ）
　　　　　　 大学生のための数学 ＞ その他の数学 ＞ 自転と公転の違いのまとめ