平行四辺形の条件 ：
　　　　　　　ＡＤ ‖ ＢＣ　かつ　ＡＤ ＝ ＢＣ　かつ　ＡＢ ‖ ＤＣ　かつ　ＡＢ ＝ ＤＣ
　　　　　　　　　　　　　　　　　　　　または、
　　　　　　　∠ＡＢＣ ＝ ∠ＣＤＡ　かつ　∠ＢＡＤ ＝ ∠ＤＣＢ


【 問 題 １ 】

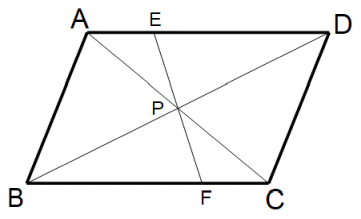
平行四辺形の対角線は互いに中点で交わることを証明せよ。

　【 解 答 】

∠ＡＢＣ ＝ ∠ＣＤＡ　と　∠ＡＤＢ ＝ ∠ＣＢＤ　より、
　　　∠ＡＢＰ ＝　∠ＣＤＰ
∠ＢＡＤ ＝ ∠ＤＣＢ　と　∠ＡCＢ ＝ ∠ＣAＤ　より、
　　　∠ＢＡＰ　＝　∠ＤＣＰ
∠ＡＰＢ ＝ ∠ＣＰＤ
ＡＢ ＝ ＣＤ
よって、 △ＡＢＰ と △ＣＤＰ は合同である。
よって、 ＢＰ ＝ ＤＰ　かつ　ＡＰ ＝ ＣＰ
したがって、　平行四辺形の対角線は互いに中点で交わる。

【 問 題 ２ 】

平行四辺形の対角線の交点を通る直線は平行四辺形の面積を２等分することを証明せよ。

　【 解 答 】

問 題 １ で証明したように、 △ＡＢＰ と △ＣＤＰ は合同である。
∠ＡＤＢ ＝ ∠ＣＢＤ　かつ　∠ＢＦＥ ＝ ∠ＤＥＦ　かつ　∠ＥＰＤ ＝ ∠ＦＰＢ　かつ　ＢＰ ＝ ＤＰ　より
　　　△ＢＦＰ と △ＤＥＰ は合同である。
∠ＡＥＦ ＝ ∠ＣＦＥ　かつ　∠ＡＣＢ ＝ ∠ＣＡＤ　かつ　∠ＡＰＥ ＝ ∠ＣＰＦ　かつ　ＡＰ ＝ ＣＰ　より
　　　△ＡＰＥ と △ＣＰＦ は合同である。
よって、 □ＡＢＦＥ と □ＣＤＥＦ　は合同である。
よって、 平行四辺形の対角線の交点を通る直線は平行四辺形の面積を２等分する。