【 問 題 】

　　　

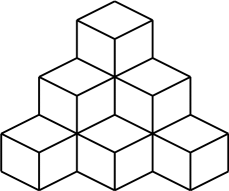
上図のようにして 1 個の体積が 1 cm³ の立方体を n 段積み上げたときの表面積を求めよ。

【 解 答 】

真上から見えるのは下図のような全て底面に平行な正方形が 6 個 敷き詰められた図です。

n ＝ 3 のとき
　　　

正方形の 1 辺の長さは 1 cm です。
他の 5 方向（ 下 左 右 前 後 ）から見てもこれと同様のことが言えます。
（ 鏡像となる場合もありますが・・・ ）
1 方向から見た表面積の大きさは 1 ＋ 2 ＋ 3 ＋ ・・・ ＋ n ＝ n(n+1)/2 cm²　です。
ということは、求める表面積は　3n(n+1) cm²　です。

【 備 考 】

　「 上図のようにして立方体を n 段積み上げたときの立方体の個数を求めよ。」 という問題の答えは、
n(n+1)(n+2) / 6 になります。それに関しては、数理論 ＞ 平方数列の和 をご覧ください。