（ 問題 ）

　 ある についての二次方程式の２つの解は、 たし合うと になり、 かけ合うと 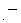になるという。 その二次方程式と２つの解を示しなさい。

（ 解答 ）

　　　　　　 ２つの解を と とします。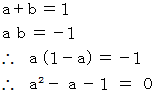
　　　　　　　　　　
　　　　　　　　　　
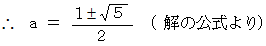
　　　　　　 したがって、 答えは
　　　　　　　　　　　　　　

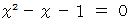
　 上記の正の解を とすると、 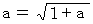が成り立ちますので、 次の式が成り立ちます。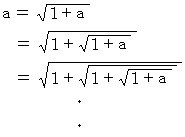

　　　　　　
　　　　　　

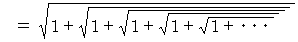
これは、 「 黄金比のフルクタル的振る舞い 」 の１つです。

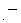
上記の負の解に をかけると 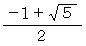になり、 正の解の逆数になります。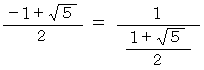
　　　　
したがって、 次の式が成り立ちます。
　　　　
　　　　
　　　　
　　　　

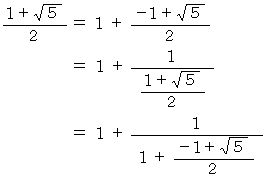
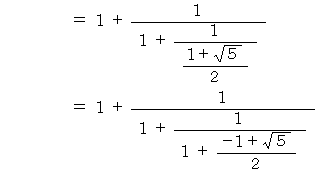
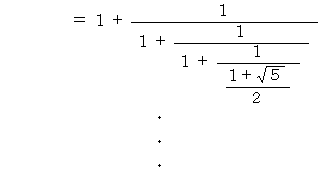
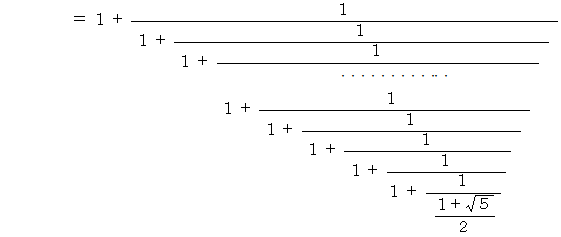
これも 「 黄金比のフルクタル的振る舞い 」 の１つです。

上の式の一番最後から２つ目の分数の影響は少ないので とすると次のようになります。
　　　　

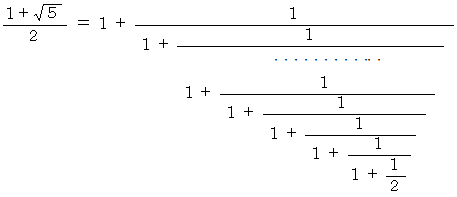
この連分数を分数に変換すべく次のようにしていきます。
　　　　
　　　　
　　　　

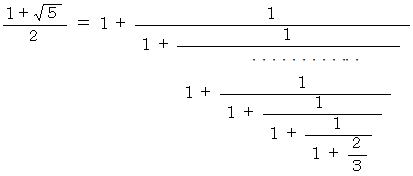
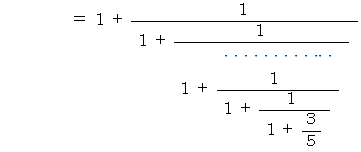
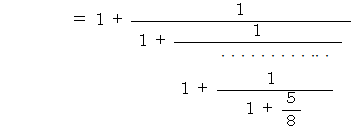
途中で変形された式の一番最後の分数で数列を作ると、 次のようになります。
　　　　　　

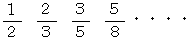
　 この数列の数の分子は前項の数の分母であり、 分母は前項の数の分子と分母とを加えたものになっています。 したがって、 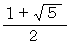の近似値を求めるプログラムは次のようになります。

　　　10　LET N = 1
　　　20　LET M = 2
　　　30　FOR I = 1 TO 470
　　　40　 LET L = N
　　　50　 LET N = M
　　　60　 LET M = M + L
　　　70　NEXT I
　　　80　PRINT USING "#.##############": 1 + N/M ;
　　　90　END

　

　

　 この無理数は、 黄金比と言われます。 数なのに名前に 「 比 」 が付いているのは、 正五角形の辺の長さに対する対角線の長さの比がこの数になっているからです。 また、次のような事実があることもその理由の１つになっています。
　 縦の長さが 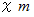、 横の長さが 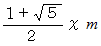の長方形の１片を完全に含む面積が 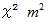の正方形を切り取った残りは、 縦の長さが 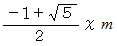、 横の長さが 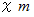の長方形です。 これは切り取る前の長方形と相似の関係になります。 これも 「 黄金比のフルクタル的振る舞い 」 の１つです。
　 こうなるのは、 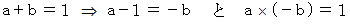　のためです。 具体的に見てみると、 次のようになります。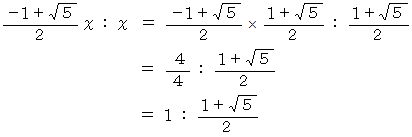
　　　　

　 ちなみに、 コピー用紙の縦横比は で黄金比とは関係ありません。 コピー用紙の縦横比のルーツについては、 株式会社トヨシコーさんのホームページをご覧になるといいと思います。
　　　　　　http://aaatoyo.com/dictionary/size.htm


さて、 黄金比の小数を連分数に変換してみます。

　　　　

したがって、 黄金比を連分数で表すと次のようになります。
　　　　

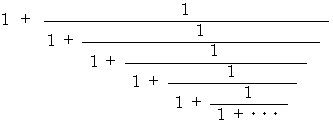
黄金比は 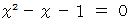の解です。 この２次方程式は次のように変形されます。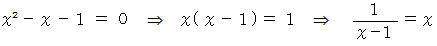
　　　　
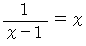　 　より、 連分数に変換しようとした時になんで無限ループに入ってしまったのか解りました。