（ 問 題 ）

　２つの変数 x と y についての比例の関係を表す関数が　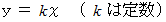　で表されることを証明せよ。

（ 証 明 ）

まず、 比についての一般的な定理を確認する。
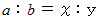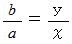
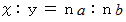
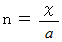　　　　 のとき、
　　　　　　　
　　　　　　　
　　　　　　　　　　 のとき、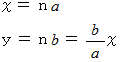
　　　　　　　　　　　　　
次に、 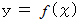とおく

２つの関連性変数群 x と y が比例しているための必要十分条件は、 次の式が成り立つことである。
　　　　
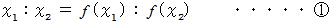
したがって、
　　　　
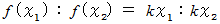
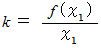　　　　　　　 のとき、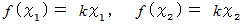
　　　　　　　　　　
　　　　　　　　　　したがって、 一般に　
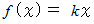
　　　　　　　　　　したがって、　

（ 追 伸 ）

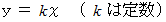
より
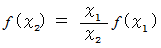　　　ですが、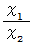
　　　　　　 は定数ではありません。

（ 反比例 について ）

　 ２つの変数 x と y についての反比例 （ 逆比例 ） の関係を表す関数は、 次の式で表されるのではありません。
　　　　　
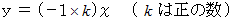
正解は次の式です。
　　　　　
　 ２つの関連性変数群 x と y が反比例しているための必要十分条件は、 次の式が成り立つことです。
　　　　　
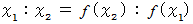
したがって、 次の式が成り立ちます。
　　　　　
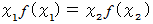
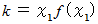とおくと、 一般に次の式で表されます。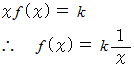
　　　　　
反比例の関係を表すグラフは、 双曲線になります。