【 問 題 】

　長方形は「全ての角が等しい四角形」であり、菱形は「全ての辺の長さが等しい四角形」である。長方形も菱形も平行四辺形であり、長方形でもあり菱形でもあるのがで正方形である。

　　　　

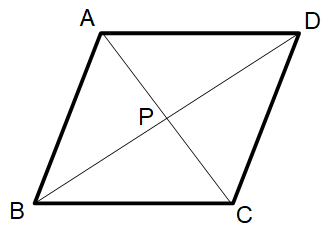
　上記の菱形の定理より、菱形の対角線は垂直に交わることを証明せよ。

【 解 答 】

　上記の菱形の定義から言えることは、三角形ＡＢＤ と 三角形ＣＤＢ は合同な二等辺三角形であということである。二等辺三角形の頂点（ 等しい長さの辺の端点が重なった点 ）と対辺の中点を結ぶ線分は、元の二等辺三角形を合同なt直角三角形に２等分する線分である。したがって、二等辺三角形の頂点と対辺の中点を結ぶ線分は、二等辺三角形の頂点の対辺と垂直に交わる。したがって、点Ｐは対角線ＢＤの中点であり、４つの直角三角形 ＡＢＰ、ＣＢＰ、ＣＤＰ、ＡＤＰ は合同な直角三角形であることが分かる。というわけで、菱形の対角線は垂直に交わることが分かった。

　このように菱形の対角線は中点どうしで交わっているが、長方形の対角線も中点どうしで交わっていて、その上に長さが等しくなっている。ただし、長方形の対角線は、菱形のように直交することは稀で、対角線が直交する長方形は正方形である。