丂儂僀僿儞僗偺尨棟 偲偼乽 攇柺偺奺揰偐傜慺尦攇偑惗偠丄慺尦攇偺嫟捠偡傞柺偑師偺攇柺偵側傞丅乿偲偄偆傕偺偱偡丅儂僀僿儞僗偺尨棟偼丄攇偺夞愜偺尨棟傪愢柧偡傞摴嬶偱傕偁傝傑偡偟丄攇偺孅愜偺尨棟傪愢柧偡傞摴嬶偱傕偁傝傑偡偟丄傑偨丄攇偺斀幩偺尨棟傪愢柧偡傞摴嬶偱傕偁傝傑偡丅攇偺斀幩偵偼 擖幩妏 亖 斀幩妏 偲偄偆朄懃偑偁傝傑偡偑丄儂僀僿儞僗偺尨棟偼丄偙偺朄懃傪尒帠偵愢柧偡傞偺偱偡丅
丂丂丂
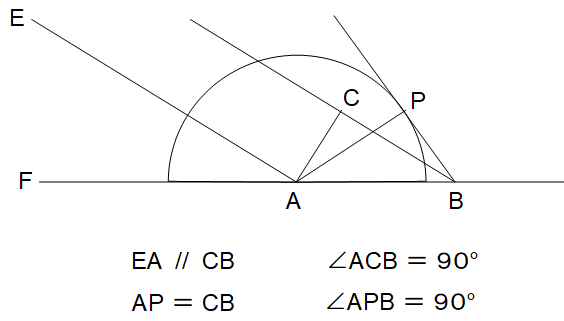
丂丂丂丂丂丂丂丂丂丂丂丂丂仸 俙俠 偲 俛俹 偼 攇柺傪昞偡慄暘偱偡丅
佢俤俙俥 亖 佢俹俙俛 偺徹柧偼丄
丂丂丂傑偢丄嶰妏宍俙俛俠 偲 嶰妏宍俛俙俹 偲偑崌摨偱偁傞偙偲傪帵偟傑偡丅
丂丂丂嶰妏宍偑崌摨偱偁傞偨傔偵偼丄師偺俁偮偺偆偪侾偮埲忋偑惉傝棫偮偙偲偱偡丅
丂丂丂丂丂嘆 俁曈偑偦傟偧傟摍偟偄
丂丂丂丂丂嘇 俀曈偲偦偺娫偺妏偑偦傟偧傟摍偟偄
丂丂丂丂丂嘊 侾曈偲偦偺椉抂偺妏偑偦傟偧傟摍偟偄
丂丂丂捈妏嶰妏宍偑崌摨偱偁傞偨傔偵偼丄師偺俀偮偺偆偪侾偮埲忋偑惉傝棫偮偙偲偱偡丅
丂丂丂丂丂嘋 幬曈偲懠偺侾曈偑偦傟偧傟摍偟偄
丂丂丂丂丂嘍 幬曈偲侾塻妏偑偦傟偧傟摍偟偄
丂丂丂嘍 傪枮偨偡嶰妏宍偼丄巆傝偺塻妏傕摍偟偄偺偱丄嘊 傪枮偨偟偰崌摨偱偡丅
丂丂丂嘋 傪枮偨偡俀偮偺崌摨側嶰妏宍傪偔偭偮偗傞偲丄俀偮偺嶰妏宍偺幬曈傪俀曈偲偡傞
丂丂擇摍曈嶰妏宍偲側偭偰侾塻妏偑摍偟偄偙偲偑暘偐傝丄嘍 傪枮偨偡偙偲偵側傝傑偡丅
-
丂偲偄偆傢偗偱丄 嶰妏宍俙俛俠 偲 嶰妏宍俛俙俹 偼 捈妏嶰妏宍偱丄幬曈 俙俛 亖 俛俙 偱丄懠偺侾曈 俙俹 亖 俛俠 傛傝丄嶰妏宍俙俛俠 偲 嶰妏宍俛俙俹 偲偑崌摨偱偁傞偲尵偊傞丅偟偨偑偭偰丄佢俹俙俛 亖 佢俠俛俙丅俤俙偲俠俛偑暯峴側偺偱丄佢俤俙俥 亖 佢俠俛俙丅傛偭偰丄佢俤俙俥 亖 佢俹俙俛 乮 徹柧廔傢傝 乯丅
 婔壗妛 傊栠傞
婔壗妛 傊栠傞