【 問 題 】

　 地球を半径 ｒ の正球体と仮定し、 地面は平らで障害物はないものとする。 北半球に緯度が等しくて経度が 180度 異なる２点がある。 この間を地上または海上を通って指定された一定の速さで移動する。 そのとき、 次のような２つのルートが与えられている。
　　　Ａルート ：　経度の等しい所を伝わって東へ東へと移動する
　　　Ｂルート ：　北極点までは北へ北へと進み、それからは南へ南へと進む
このとき、 Ｂルートの移動時間 が Ａルートの移動時間 を決して超えることはないことを証明せよ。

【 解 答 】

２つの地点の緯度をラジアンに換算した値を θ（ ０ ≦ θ ≦ π/２ ） とすると、
　　　

　　　
　　　
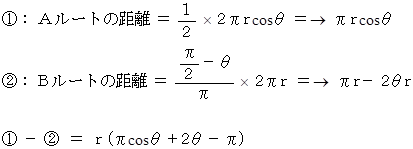
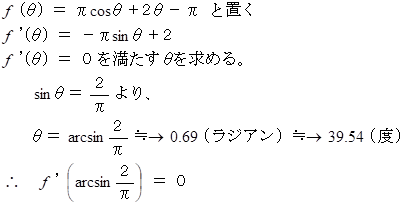
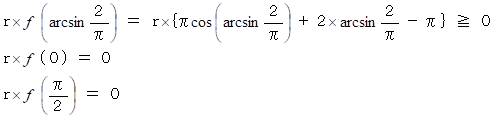
　 よって、 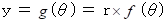のグラフは、 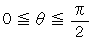の範囲では、 上に凸で、
　ことが解った。
　 したがって、
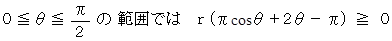
　 したがって、 Ｂルートの距離がＡルートの距離を決して超えることはない。
　 したがって、 一定の速さで移動するのだから、 Ｂルートの移動時間 が Ａルートの移動時間 を決して超えることはない。