集合Aの要素の数を
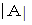 で表します。 次の式は、 交わり合っている3つの集合の包除原理を表しています。
で表します。 次の式は、 交わり合っている3つの集合の包除原理を表しています。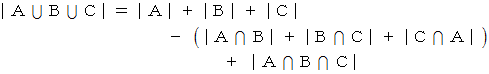
交わっている4つの集合の包除原理を次のようになります。
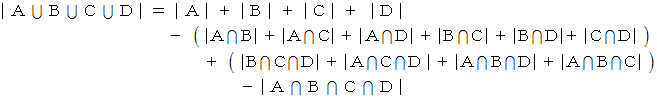
交わっている集合が5つ以上の場合でも、 同様にして、 どれかの集合に属している要素の数を求めることができます。
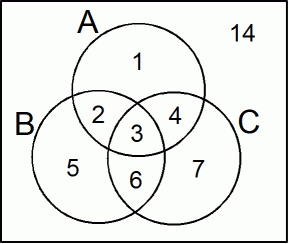
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
10 + 16 + 20 − ( 5 + 9 + 7 ) + 3 = 28
では、 90と互いに素で、 90を超えない自然数の数を求めてみましょう。
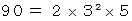 ですから、 90未満の自然数のうち、2の倍数でもなく、3の倍数でもなく、5の倍数でもない数の数を求めればいいことになります。
ですから、 90未満の自然数のうち、2の倍数でもなく、3の倍数でもなく、5の倍数でもない数の数を求めればいいことになります。2の倍数の数: 45個
3の倍数の数: 30個
5の倍数の数: 18個
6の倍数の数: 15個
15の倍数の数: 6個
10の倍数の数: 9個
30の倍数の数: 3個
したがって、 求める数は次のようになります。
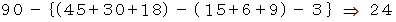
3つの異なる素数の重複を認める積の形で表される自然数
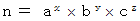 について、 オイラーは、 その自然数と互いに素でありその自然数を超えない自然数の数
について、 オイラーは、 その自然数と互いに素でありその自然数を超えない自然数の数 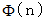 を求める公式を導いています。
を求める公式を導いています。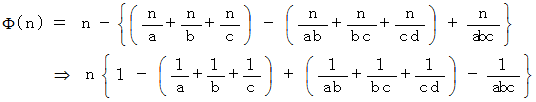
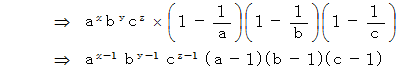
これを一般化して、 ある自然数について、 その自然数と互いに素でありその自然数を超えない自然数の数を求めるプログラムを十進BASIC で作ってみました。
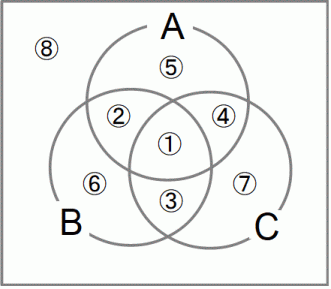

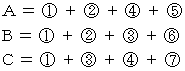
A または B または C は、 次の式から求めることができます。
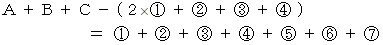
 論理学 へ戻る
論理学 へ戻る