【 問 題 】

　 放物線と一本の直線とで囲まれる部分が左右対称であるとき、 その中にできる最大の三角形の面積は放物線と直線とで囲まれる部分の面積の ４分の ３ を占めることを証明せよ。

【 解 答 】

　　　　　

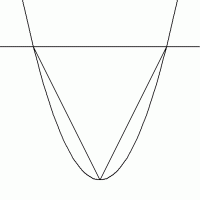
　 放物線と直線とで囲まれる部分が左右対称であるとき、その中にできる最大の三角形は、 二等辺三角形で頂点は放物線の頂点に一致する。

　 ここで、 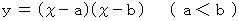　という放物線を考える。 この放物線と x 軸とで囲まれる部分は左右対称である。



　 したがって、 この放物線と x 軸とで囲まれる部分の中にできる面積が最大の二等辺三角形の底辺の長さは 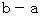で、 高さは 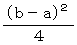になる。 したがって、 その面積 （ ｓ ） は次のようになる。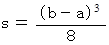
　　　　　

　 一方、 放物線と直線とで囲まれる部分の面積 （ Ｓ ） は、 公式より次のようになる。
　　　　　
　 したがって、
　　　　　

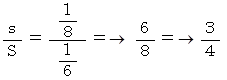
　 そういうわけで、 この三角形の面積は放物線と直線とで囲まれる部分の面積の ４分の３ を占めることが判った。