( 問 題 )
-
縦の長さ < 横の長さ で、 その辺が方眼紙の格子線上にある長方形を思い浮かべてください。 この長方形が抱える横の方眼数を
 個、 縦の方眼数を
個、 縦の方眼数を  個 とします。 さて、 この長方形の1本の対角線が通る方眼の数はいくつでしょうか?
個 とします。 さて、 この長方形の1本の対角線が通る方眼の数はいくつでしょうか?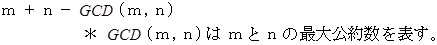
( 解 説 )
-
長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) の数を
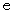 とすると、
とすると、 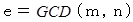 になることを、 まず説明します。
になることを、 まず説明します。長方形の左下を原点とすると、対角線の方程式は次のように表されます。
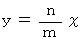

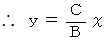
したがって、 次の式を満たす点
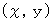 は、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) になります。
は、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) になります。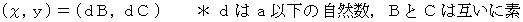
 以下の自然数の数は
以下の自然数の数は  個です。 したがって、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) の数が、 すなわち
個です。 したがって、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) の数が、 すなわち 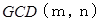 になります。 つまり、
になります。 つまり、 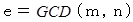 になります。
になります。次に、
 と
と  を足した数から、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) を引いた数が、 対角線が通る方眼の数になることを説明します。
を足した数から、 長方形の辺を含む内部で対角線が通る格子点 ( 原点は含まない ) を引いた数が、 対角線が通る方眼の数になることを説明します。対角線を原点からなぞっていって、 通過した方眼の数を数えることにします。 ちょうど横に1マス分なぞったときに、 横に走る格子線のどれかと出会うかどうかで、 横に1マス分対角線をなぞったときに通過した方眼の数が1個なのか2個なのかが決まります。 ただし、 縦に走る格子線を離れた直後から次の縦に走る格子線と交わる寸前の間に、 横に走る格子線と交わるかどうかで判断しなければなりません。
そうしますと、 最高で

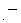
 回、 ちょうど横に1マス分対角線をなぞったときに横に走る格子線のどれかと出会うことになります。 そしてその回数は次のようになります。
回、 ちょうど横に1マス分対角線をなぞったときに横に走る格子線のどれかと出会うことになります。 そしてその回数は次のようになります。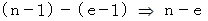
したがって、 最後まで対角線をなぞったときに通過した方眼の数は次のようになります。
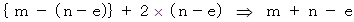
最後に、 以上の2つの事をまとめると、 対角線が通る方眼の数は次のように表されることが解ります。
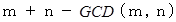
 その他の数学 へ戻る
その他の数学 へ戻る