（１） 相対的自転

　「 Ａ君とＢ君は向かい合っています。 その後、Ａ君は反時計回りに１自転しました。 といことは、Ａ君にとってＢ君は、 自分の方を向いたまま自分の周りを時計回りに１公転したことになります。 ということは、 Ｂ君はＡ君にとって時計回りに１自転したことにもなります。」と言いますと、「 公転したのは解るけども、 自転はしていないと思うわ。 だって、 Ｂ君の背中は絶対にＡ君から見えないんだもの。」という反論が返ってきます。

　「 Ａ君は固有の３次元座標系を持っていて、 その原点に存在していて、 360 度の空間すべてを同時に観察することができる。」と考えてください。 Ａ君の座標系からすれば、 Ｂ君は常に向きを変化させていますので、 相対的にＢ君は自転しています。 しかし、Ｂ君は同時に公転しているので、 常にＡ君から自分の背中が見えない位置に移動し続けています。 そういうわけで、 Ｂ君はＡ君にとって相対的に自転しているのです。

（２） 自転の方向は観察者によって異なる

　 両手でボールペンを持ってください。 ボールペンの先が下を向くように。
　 反時計回りにボールペンを軸回転（ 軸型自転 ）させてください。
　 それを続けながら、 ボールペンを逆さにしてください。
　 すると、 ボールペンは時計回りになります。
　 ボールペンの頭が見えるようにして逆さにすると、 比較的遅い時点で回転方向が変わります。

　　 ボールペンの軸型自転を回転ベクトル（ 右ネジの法則に従う矢印 ）で表すと、
　 その回転ベクトルの向きが反転するのです。

（３） 軸型自転（ 重心水平軸回転 ） と プロペラ型自転（ 重心垂直軸回転 ）

　 レコード盤の上にボールペンを置きます。
　 ボールペンの中央がレコードの中心に位置するように。
　 レコードを１回転させます。
　 すると、 ボールペンは１回 プロペラ型自転 をします。

　 レコード盤の上にボールペンを置きます。
　 ボールペンの先がレコードの中心を向くように。
　 レコードを１回転させます。
　 すると、 ボールペンはレコードの中心を中心に１回公転をします。
　 と同時に、 ボールペンは１回 プロペラ型自転 をします。

　 レコード盤の上にボールペンを垂直に立てて固定します。
　 ボールペンの先を下にして。
　 レコードを回転させます。 反時計回りに角速度の大きさ ω で。
　 すると、 ボールペンはレコードの中心を中心に公転をします。 反時計回りに角速度の大きさ ω で。
　 と同時に、 ボールペンは軸型自転をします。 反時計回りに角速度の大きさ ω で。

　 レコード盤の上にボールペンを斜め45度に倒して固定します。
　 ボールペンの先を下に、 頭がレコードの中心を通る垂線を向くようにして。
　 レコードを回転させます。 反時計回りに角速度の大きさ ω で。
　 すると、 ボールペンはレコードの中心を中心に公転をします。 反時計回りに角速度の大きさ ω で。
　 と同時に、 ボールペンは軸型自転をします。 反時計回りに角速度の大きさ 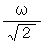で。
　 と同時に、 ボールペンはプロペラ型自転をします。 反時計回りに角速度の大きさ 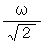で。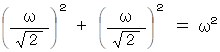
　　　　　　　　　　　

　 最後の部分は非常に分かりにくいと思います。 その理由を知りたい方は、 次の論文を見てください。
　　　　大学生のための数学 ＞ その他の数学 ＞ ３次元空間における微小直線分の回転運動
　　　　大学生のための物理学 ＞ 力学 ＞ フーコーの振り子（ 入門編 ）