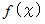 を
を  で割ると、 商が
で割ると、 商が 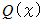 で、 余りが
で、 余りが 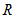 でした。 これを式で表すと次のようになります。
でした。 これを式で表すと次のようになります。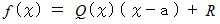
この式に
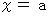 を代入すると、 次のようになります。
を代入すると、 次のようになります。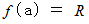
以上のことより、 「
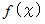 を
を  で割った余りは
で割った余りは 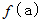 である。」 ということができます。 これを 「 剰余定理 」 といいます。
である。」 ということができます。 これを 「 剰余定理 」 といいます。剰余定理を用いなければならない過去の入試問題には、 次のようなものがありました。
整式
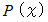 を
を 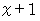 で割った余りが
で割った余りが  であり、
であり、 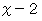 で余りが 4 であるとき、
で余りが 4 であるとき、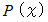 を
を 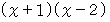 で割ったときの余りを求めよ。 ( 2010年 京都産業大 )
で割ったときの余りを求めよ。 ( 2010年 京都産業大 )( 解 答 )
-
剰余定理より、
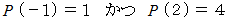 である。 ・ ・ ・ ・ ・
である。 ・ ・ ・ ・ ・ 
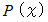 を
を 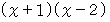 で割ったときの 商を
で割ったときの 商を
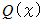 余りを
余りを 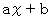 とおくと、
とおくと、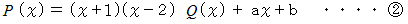
 より、
より、 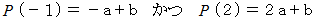 である。
である。 と
と  より、
より、 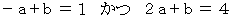 である。
である。したがって、
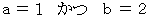 である。
である。したがって、 答えは
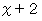 である。
である。 その他の数学 へ戻る
その他の数学 へ戻る