剰余数の性質
 数理論 へ戻る
数理論 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2014.10.20____
ここに登場するアルファベットは、 特に指定のない限り、 正の整数を表すものとします。
(00) n で割ると m 余る数(B)に n を加えた数を n で割った余りは m である。
解 説 :
乗余数の性質の基本です。
MOD ( B , n ) = m MOD ( B , n ) = MOD ( B+n , n ) = m
B ≡ B+n ≡ m ( mod n )
(01) n で割ると m 余る数(B)に k を加えた数を n で割った余りは、 m に k を加えた数を n で割った余りに等しい。
解 説 :
乗余数の性質の基本です。
MOD ( B , n ) = m MOD ( B+k , n ) = MOD ( MOD ( B , n )+k , n ) = MOD ( m+k , n )
B ≡ m ( mod n ) B+k ≡ m+k ( mod n )
(02) n で割ると m 余る数(B)に A をかけた数を n で割った余りは、 m に A をかけた数を n で割った余りに等しい。
解 説 :
乗余数の性質の基本です。
MOD ( B , n ) = m MOD ( A×B , n ) = MOD ( A × MOD ( B , n ) , n ) = MOD ( A×m, n )
B ≡ m ( mod n ) A×B ≡ A×m ( mod n )
(1) n で割ると 1 余る数(B)は、 何乗しても n で割ると 1 余る。
解 説 :
K を任意の自然数とする。
MOD ( B , n ) = 1 MOD ( B , n ) = MOD ( BK , n ) = 1
B ≡ 1 ( mod n ) B ≡ BK ≡ 1 ( mod n )
n で割ると1余る数は、 0 以上の整数 m を使うと、 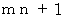 で表されます。
で表されます。
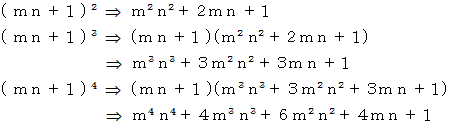
5乗以上の展開については、 次の2項定理を利用すると、 簡単です。
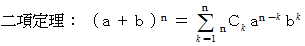
すべて最後の項以外は n で割り切れますので、 何乗しても余りは 1 になることが解かります。
(2) n で割ると A 余る数(B)を K乗した数を n で割った余りは A をK乗した数を n で割った余りに等しい。
解 説 :
MOD ( B , n ) = A MOD ( BK , n ) = MOD ( AK , n )
B ≡ A ( mod n ) BK ≡ AK ( mod n )
Q と W を 0 以上の整数とします。 n で割ると A 余る数を nQ+A と nW+A とします。 2項定理を使って K乗 した数を展開しますと、 〇×n の形になっていない項はどちらも 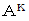 だけです。 これは(1)を拡張して一般化したものです。
だけです。 これは(1)を拡張して一般化したものです。
(3) 素数 S で割ると A 余り、 素数 T で割ると A 余る数(B)は、 ST で割ると A 余る。
解 説:
MOD ( B , S ) = A MOD ( B , T ) = A MOD ( B , ST ) = A
B ≡ A ( mod S ) B ≡ A ( mod T ) B ≡ A ( mod ST )
0 以上の整数 m を使うと、 素数 S で割ると A 余り、 素数 T で割ると A 余る数は、 mST+A で表されます。 したがって、 この数を ST で割ると A 余ります。
(4) n で割ると A 余る数(C)と n で割ると B 余る数(D)がある。 この2つの数を加えた数を n で割った余りは、 A+B を n で割った余りに等しい。
解 説 :
MOD ( C , n ) = A MOD ( D , n ) = B MOD ( C+D , n ) = MOD ( A+B , n )
C ≡ A ( mod n ) D ≡ B ( mod n ) C+D ≡ A+B ( mod n )
Q と W を 0 以上の整数とします。 n で割ると A 余る数を nQ+A とし、 n で割ると B 余る数を nW+B とします。 2つの数を加えると n(Q+W)+(A+B) になります。 この数の第1項は n で割り切れますので、 この数を n で割った余りは、 第2項の A+B を n で割った余りになります。
(5) n で割ると A 余る数(C)と、 n で割ると B 余る数(D)がある。 この2つの数をかけた数を n で割った余りは、 AB を n で割った余りに等しい。
解 説:
MOD ( C , n ) = A MOD ( D , n ) = B MOD ( CD , n ) = MOD ( AB , n )
C ≡ A ( mod n ) D ≡ B ( mod n ) CD ≡ AB ( mod n )
Q と W を 0 以上の整数とします。 n で割ると A 余る数を nQ+A とし、 n で割ると B 余る数を nW+B とします。 2つの数をかけると 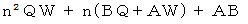 になります。 この数の第1項と第2項は n で割り切れますので、 この数を n で割った余りは、 第3項の AB を n で割った余りになります。
になります。 この数の第1項と第2項は n で割り切れますので、 この数を n で割った余りは、 第3項の AB を n で割った余りになります。
(6) 複数の n で割り切れない自然数の積を n で割った余りは、 それぞれの数を n で割った余りの積を n で割った余りに等しい。
解 説 :
これは(5)を拡張して一般化したものです。
(7) 素数 S と S の倍数でない 数 H があるとき、 HS−1 を S で割った余りは 1 である。
(8) 数 H が 素数 S とも 素数 T とも互いに素のとき、 H(S−1)(T−1) を ST で割った余りは 1 である。
解 説 :
これは、 N = ST のときのオイラーの定理です。 オイラーの定理とは次のようなものです。
「 ある正の整数  よりも小さくて、 かつ、
よりも小さくて、 かつ、  と互いに素の正の整数の数(かず)を
と互いに素の正の整数の数(かず)を 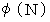 で表すとき、
で表すとき、 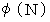 と互いに素の任意の正の整数
と互いに素の任意の正の整数  について、
について、 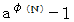 は必ず
は必ず  で割り切れる。」
で割り切れる。」
※ 数理論 > オイラーの定理
(9) n = ST ( S と T は 素数 ) のとき、 n よりも小さな数 H の K乗 ( ただし、 K は (S−1) と (T−1) の最小公倍数の倍数 ) を n で割った余りは 1 である。
解 説 :
この性質は、 RSA暗号に用いられています。
(10) n と n よりも大きくない数 m があるとき、 n の階乗に m を加えた数を m で割った余りは 0 である。
解 説 :
MOD ( n!+m , m ) = 0
n!+m ≡ 0 ( mod m )
n の階乗は m の倍数です。
(11) aP ≡ aR ( mod b ) で、a と b が互いに素ならば、 P ≡ R ( mod b ) である。
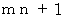 で表されます。
で表されます。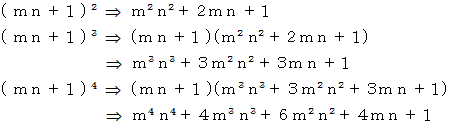
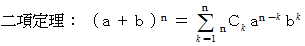
 数理論 へ戻る
数理論 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る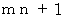 で表されます。
で表されます。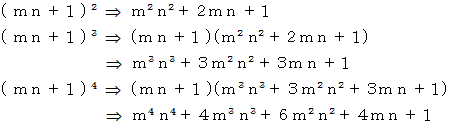
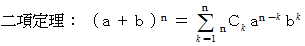
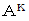 だけです。 これは(1)を拡張して一般化したものです。
だけです。 これは(1)を拡張して一般化したものです。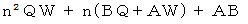 になります。 この数の第1項と第2項は n で割り切れますので、 この数を n で割った余りは、 第3項の AB を n で割った余りになります。
になります。 この数の第1項と第2項は n で割り切れますので、 この数を n で割った余りは、 第3項の AB を n で割った余りになります。 よりも小さくて、 かつ、
よりも小さくて、 かつ、  と互いに素の正の整数の数(かず)を
と互いに素の正の整数の数(かず)を 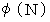 で表すとき、
で表すとき、 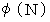 と互いに素の任意の正の整数
と互いに素の任意の正の整数  について、
について、 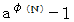 は必ず
は必ず  で割り切れる。」
で割り切れる。」