２次元直交座標系に散在する点たちの重心を通り、 回帰直線に近い直線で、 その直線で点たちの左右の重心のバランスが取れる。 そんな直線は、 左側の点の直線からの距離の平均 と 右側の点の直線からの距離の平均 が等しくなっている。 この直線を 「 重心直線 」 と呼ぶことにしよう。
　 重心直線の近似を求めるプログラムを作ってみた。 まず回帰直線を求めて、 その近くを通る直線ごとに、 左側の点の直線からの距離の平均 と 右側の点の直線からの距離の平均 の差を求めて、 最も少ない所を探っていく方法である。


Data = [ [−1,3], [−3,5], [−4,5], [−6,9], [−7,8] ]

回帰直線は、
傾きが で、
y 軸上の y 座標値 を通る直線である。

重心直線は、
傾きが で、
y 軸上の y 座標値 を通る直線である。

２つの直線は、 重心点 （ ，　 ） を通る。

　　　　　　　　　　　　　　− 回帰直線　　　− 重心直線
　　　　　　

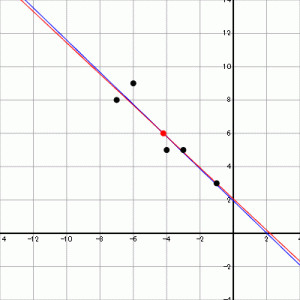
　 回帰直線については、 大学生のための数学 ＞ 確率と統計学 ＞ 相関関係の解析　をご覧ください。 点と直線の距離については、 大学生のための数学 ＞ その他の数学 ＞ 点から直線までの距離　をご覧ください。