【 問 題 】

　平行四辺形ＡＢＣＤを描いた下図において、 ３ＢＰ ＝ ＢＤ　を示せ。

　　　

【 解答 その１ 】

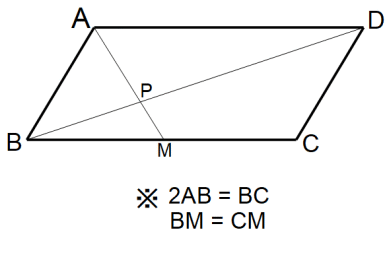
　同じ幅に並んでいるたくさんの平行線に交わる１本の直線は、それらの平行線によって均等な長さに分割されます。
この原理を用いて証明します。
　　　

ＡＮ ＝ ＤＮ ＝ ＢＭ より、４本の平行線の隣同士の間隔は均一である。
したがって、線分ＢＤはこれらの平行線らによって３等分されている。
よって、 ３ＢＰ ＝ ＢＤ　である。

【 解答 その２ 】

　点Ａに物質Ａが存在し、点Ｍに物質Ｂが存在しているとする。物質Ａの質量と物質Ｂの質量の比は 1：2 とする。
すると、物質Ａと物質Ｂの系の重心が点Ｐになる。
なぜなら、Ｂを原点としたときに、重心ベクトル 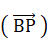は次のように表されるからである。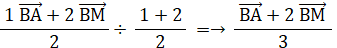

　　　

また、次の式が成り立っている。
　　　
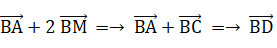
よって、
　　　
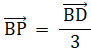
よって、 ３ＢＰ ＝ ＢＤ　である。