階乗を含んでいる数列には次のようなものがあります。
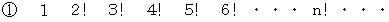

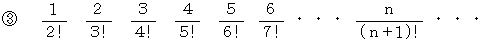
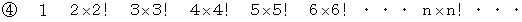
(1)
 について
について-
6項までの和は 5309 ですが、 それを導いてみましょう。
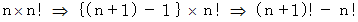 ですから、
ですから、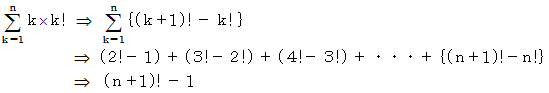
したがって、
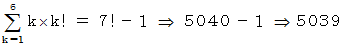
というわけでしたが、 さて、
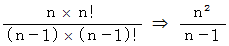 ですから、 漸化式は次のようになります。
ですから、 漸化式は次のようになります。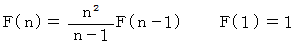
そこで、 次のような十進BASIC のプログラムを作って実行すると、 6項までの和は 5309 であることが解ります。
 について
について-
6項までの和は
 で、 無限大項までの和は
で、 無限大項までの和は  ですが、 それを導いてみましょう。
ですが、 それを導いてみましょう。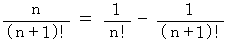 ですから、
ですから、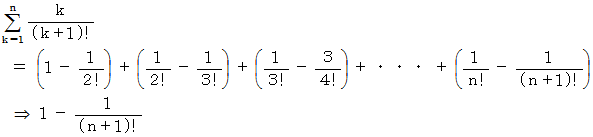
したがって、

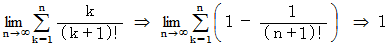
というわけでしたが、 さて、
 ですから、 漸化式は次のようになります。
ですから、 漸化式は次のようになります。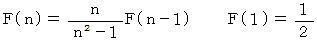
そこで、 次のような十進BASIC のプログラムを作って実行すると、 6項までの和は
 で、 無限大項までの和は
で、 無限大項までの和は  であることが解ります。
であることが解ります。 について
について-
6項までの和は
 で、 無限大項までの和は ネイピア数 ですが、 それを導いてみましょう。
で、 無限大項までの和は ネイピア数 ですが、 それを導いてみましょう。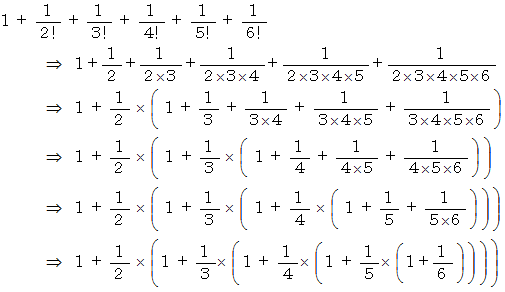
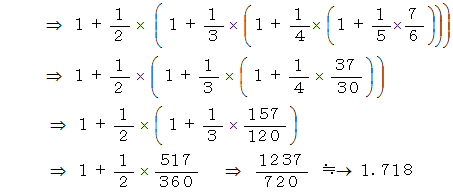
とういうことでしたが、 さて、
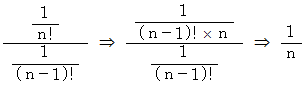 ですから、 漸化式は次のようになります。
ですから、 漸化式は次のようになります。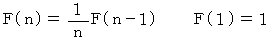
そこで、 次のような十進BASIC のプログラムを作って実行してみましょう。 すると、 6項までの和は
 で、 無限大項までの和は ネイピア数 であることが解ります。
で、 無限大項までの和は ネイピア数 であることが解ります。漸化式がなくとも、 この数列の 項 と それまでの和 を求める十進BASIC のプログラムを作ることができます。 最初にこの数列の6項までの和を変形していってフルクタル的な式を導きましたが、 それを利用するのです。
 について
について-
6項までの和は 873 ですが、 それを導いてみましょう。
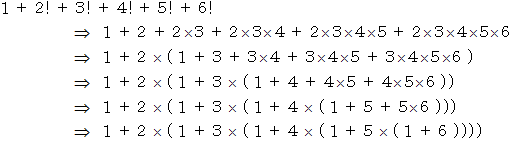
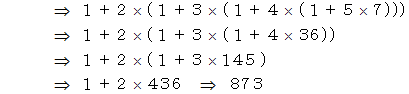
ということでしたが、 さて、 漸化式は次のようになります。
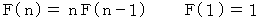
そこで、 次のような十進BASIC のプログラムを作って実行してみましょう。 6項までの和は 873 であることが解ります。
漸化式がなくとも、 この数列の 項 と それまでの和 を求める十進BASIC のプログラムを作ることができます。 最初にこの数列の6項までの和を変形していってフルクタル的な式を導きましたが、 それを利用するのです。
 数理論 へ戻る
数理論 へ戻る