(1) 表を使って階乗を素因数分解する
9! を素因数分解するのに、 次のような表を作る方法があります。
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | |
| 2 |  |
 |
 |
 |
|||||
| 4 |  |
 |
|||||||
| 8 |  |
||||||||
| 3 |  |
 |
 |
||||||
| 9 |  |
||||||||
| 5 |  |
||||||||
| 7 |  |
この表の作り方ですけれども、 1 段目に 9 〜 1 の数を並べ、 2段目に素数の2で割り切れる数に
 の印を付け、3段目に2の2乗で割り切れる数に
の印を付け、3段目に2の2乗で割り切れる数に  の印を付け、 ・ ・ ・ ・ というふうにします。
の印を付け、 ・ ・ ・ ・ というふうにします。表ができたら、 あとはそれぞれの数を数えて次のように書くと出来上がりです。
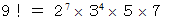
以上の原理を用いて、 階乗の素因数分解をしてくれるプログラムを 十進BASIC で作りました。
さて、 200 ! は 5で何回まで割り切ることができるでしょうか?
[ 200 / 5 ] + [ 200 / 25 ] + [ 200 / 125 ] =→ 40 + 8 + 1 =→ 49
答えは 49 回です。 次のプログラムで答えを確かめてみましょう。
-
20! = 218×38×5×7×11×13×17×19
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||||||||||
| 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | |||||||||||
| 〇 | 〇 | 〇 | 〇 | 〇 | ||||||||||||||||
| 〇 | 〇 | |||||||||||||||||||
| 16 | 〇 | |||||||||||||||||||
| 〇 | 〇 | 〇 | 〇 | 〇 | 〇 | |||||||||||||||
| 〇 | 〇 | |||||||||||||||||||
| 〇 | ||||||||||||||||||||
| 〇 | ||||||||||||||||||||
| 11 | 〇 | |||||||||||||||||||
| 13 | 〇 | |||||||||||||||||||
| 17 | 〇 | |||||||||||||||||||
| 19 | 〇 |
n! = 2a×3b×5c×7d×・・・・
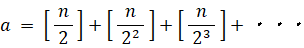
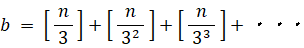
※ ガウス記号 [ ] は、中の数字を超えない最大の整数を返す関数です。
-
【 問 題 】
全体集合を自然数とする。
3m × 8n の下1桁は0でないことを証明せよ。
【 解 答 】
下1桁が0である数は 10k× a ( a は10で割り切れない数 ) と表すことができる。
つまり、 下1桁が0である数は 2k×5k× a と表すことができる。
3m × 8n には素因数の5が含まれていないので、 2k×5k× a と表すことができない。
したがって、 3m × 8n の下1桁は0でない。
ちなみに、 下1桁が0である数とは 10で割り切れる数のことである。
-
【 問 題 】
50 ! は下何桁までが0か?
【 解 答 】
50 ! を 2k×5k× a ( a は10で割り切れない数 ) の形に変形する。
50 ! を構成している要素の中に
2で割り切れる数は 2×1、2×2、・・・ 2×25 の 25 個ある。
4で割り切れる数は 4×1、4×2、・・・ 4×12 の 12 個ある。
8で割り切れる数は 8×1、8×2、・・・ 8×6 の 6 個ある。
16で割り切れる数は 16×1、16×2、16×3 の 3 個ある。
32で割り切れる数は 32×1 の 1 個ある。
これらの 「 のべの合計 」 は 47 個である。
5で割り切れる数は 5×1、5×2、・・・ 5×10 の 10 個ある。
25で割り切れる数は 25×1、25×2 の 2 個ある。
これらの 「 のべの合計 」 は 12 個である。
したがって、 50 ! = 247×512× a ( a は10で割り切れない数 )
したがって、 50 ! = 212×512× b ( b は10で割り切れない数 )
したがって、 50 ! = 1012× b ( b は10で割り切れない数 )
したがって、 50 ! は下 12 桁までが0である。
 数理論 へ戻る
数理論 へ戻る