1,2,3,・・・,m,・・・,n のn個の自然数がこの順に時計回りに並べられた円数列があります。
m と n は互いに素とします。
m の上にコマを置き、 ノートに m と記入します。 時計回りに m だけコマを進め、 止まった所の数字をノートに記入します。 これを繰り返します。
すると、 およそ m 周回ったところで、 コマは n の所に止まります。 ノートに n と記入し、 これまでに記入した数字を見てください。 1 ~ n の数字が 1 個ずつ記入されているはずです。
m と n は互いに素とします。
m の上にコマを置き、 ノートに m と記入します。 時計回りに m だけコマを進め、 止まった所の数字をノートに記入します。 これを繰り返します。
すると、 およそ m 周回ったところで、 コマは n の所に止まります。 ノートに n と記入し、 これまでに記入した数字を見てください。 1 ~ n の数字が 1 個ずつ記入されているはずです。
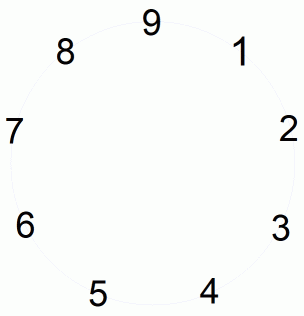
n = 9 、 m = 7 でやってみましょう。
7 5 3 1 8 6 4 2 9 ・ ・ ・

9-7 = 2 です。 7 から反時計回りに 2 ずつ移動した結果に等しくなっています。
n = 9、 m = 4 でやってみましょう。
4 8 3 7 2 6 1 5 9 ・ ・ ・

9-4 = 5 です。 4 から反時計回りに 5 ずつ移動した結果に等しくなっています。
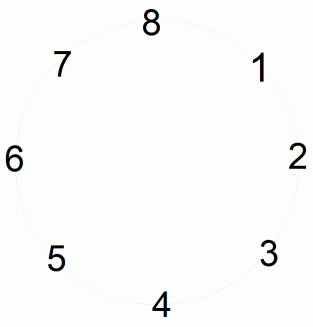
n = 8、 m = 5 でやってみましょう。
5 2 7 4 1 6 3 8 ・ ・ ・

8-5 = 3 です。 5 から反時計回りに 3 ずつ移動した結果に等しくなっています。
n = 8、 m = 3 でやってみましょう。
3 6 1 4 7 2 5 8 ・ ・ ・

8-3 = 5 です。 3 から反時計回りに 5 ずつ移動した結果に等しくなっています。
関数 M(a, b) を a を b で割ったときの余りを出力するものとします。
m < n とします。
m と n とが互いに素であるとき、
M( k × m , n ) * k = 1,2,3,・・・,n の値は、
0 ~ n-1 の整数であり、 同じ数になることはありません。
m < n とします。
m と n とが互いに素であるとき、
M( k × m , n ) * k = 1,2,3,・・・,n の値は、
0 ~ n-1 の整数であり、 同じ数になることはありません。
たとえば、 M(7, 9)= 7 ですが、
M( 1×7, 9)= 7
M( 2×7, 9)= 5
M( 3×7, 9)= 3
M( 4×7, 9)= 1
M( 5×7, 9)= 8
M( 6×7, 9)= 6
M( 7×7, 9)= 4
M( 8×7, 9)= 2
M( 9×7, 9)= 0
では、なぜそうなるのでしょう? 証明してみましょう。
m,n,a,b,c,d,k,p を自然数とします。
m,n は m < n で、互いに素であるとします。
a,b は次の①を満たすものとします。
1 ≦ a < b ≦ n ・ ・ ・ ①
m を 1倍、2倍、3倍、・ ・ ・、n 倍 した数を n で割った余りのうち、
等しいものが存在すると仮定します。
すると、 次の②と③の式を満たす a,b,c,d,k が存在することになります。
ma = nc + k ・ ・ ・ ②
mb = nd + k ・ ・ ・ ③
③ から ② を辺々引いて、
m(b-a)= n(d-c)
この式が成り立つための必要十分条件は次のようになります。
b-a = np かつ d-c = mp
そのための必要条件は次のようになります。
b = a + np
b = a + np > n だから、 ① と矛盾します。
よって、 m を1倍、2倍、3倍、・・・ n 倍した数は、n で割るとすべて余りが異なります。
関数 M(a, b) を a を b で割ったときの余りを出力するものとします。
m < n とします。
m > M(n, m) です。
m と n とが互いに素であるとき、
m と M(n, m) とは互いに素であり、 ( ユークリッドの互除法の原理より )
M( k × M(n, m), m ) * k = 1,2,3,・・・,m の値は、
0 ~ m-1 の整数であり、 同じ数になることはありません。
m < n とします。
m > M(n, m) です。
m と n とが互いに素であるとき、
m と M(n, m) とは互いに素であり、 ( ユークリッドの互除法の原理より )
M( k × M(n, m), m ) * k = 1,2,3,・・・,m の値は、
0 ~ m-1 の整数であり、 同じ数になることはありません。
たとえば、 M(9, 7)= 2 ですが、
M( 1×2, 7)= 2
M( 2×2, 7)= 4
M( 3×2, 7)= 6
M( 4×2, 7)= 1
M( 5×2, 7)= 3
M( 6×2, 7)= 5
M( 7×2, 7)= 0
参考文献 : 日常的物理学文集 > 音楽と物理学 > 五度圏 と 回転総取得条件
 数理論 へ戻る
数理論 へ戻る