（１） 基本的な数列の n 項までの和

　　　　　初項 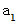公差 ｄ　の数列の n 項 までの和 ：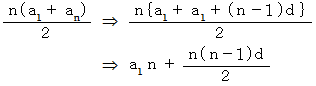
　　　　　　　　

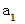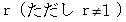　　　　　初項 公比 の数列の n 項 までの和 ：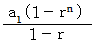
　　　　　　　　
　　　　　　　　
　　　　　　　　（ 証明 ）
　　　　　　　　

　　　　　　　　

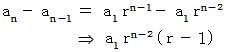
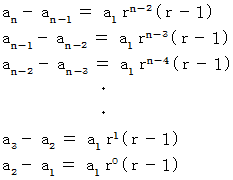
　　　　　　　　辺々加えると
　　　　　　　　



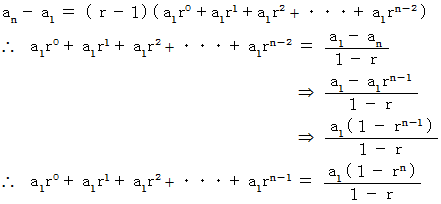
（２） 複雑な数列の n 項 を n を使って表す（ その１ ）

　　　　　次の数列の n 項 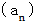を求めてみましょう。
　　　　　　　　　５　　６　　８　　12　　20　　36　　・ ・ ・ ・ ・

　　　　　階差数列は、 次のようになります。
　　　　　　　　　１　　２　　４　　８　　16　　・ ・ ・ ・ ・

　　　　　したがって、 階差数列の n 項 までの和は次のようになります。
　　　　　　　　　
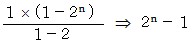
　　　　　したがって、
　　　　　　　　　



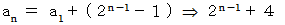
（３） 複雑な数列の n 項 を n を使って表す （ その２ ）

　　　　　次の数列の n 項 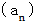を求めてみましょう。
　　　　　　　　　３　　７　　13　　21　　31　　43　　・ ・ ・ ・ ・

　　　　　階差数列は、 次のようになります。
　　　　　　　　　４　　６　　８　　10　　12　　・ ・ ・ ・ ・
　　　　　つまり、
　　　　　　　　　
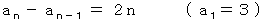
　　　　　そこで、
　　　　　　　　　
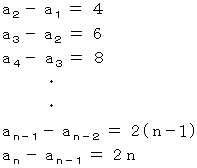
　　　　　辺々加えると、
　　　　　　　　　



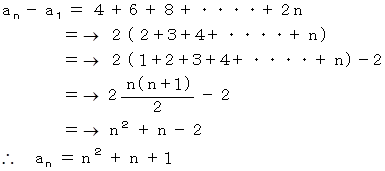
（４） 階差数列が元の数列に等しいケース

　　　　　２　　４　　８　　16　　32　・ ・ ・ ・　（ 初項２ 公比２ の等比数列 ）