（ 問 題 ）

　 単位格子が書かれている方眼紙があります。 格子線上に辺がくるようにして、 一辺の長さが ｎ マスの正方形を描きます。
　 この正方形の左上の頂点から出発して、 格子線上を移動しながら正方形に含まれている全ての格子の交点を通ってから元の位置に戻るとき、 最短ルートの道のりは何マスになるでしょうか？

（ 解 答 ）

　 同じ交点をなるべく通らないようにするのが最短です。 したがって、 一辺の長さが 奇数マス と 偶数マス では、 図のように異なります。

　　　　　

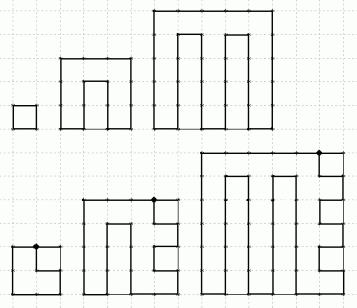
　 奇数マスのときは、 一辺の長さが２マスずつ大きくなるにつれ、 最短ルートの道のりは、 一辺の長さが １ マスの正方形の場合から、 次のように増えていきます。 それは、 正方形に含まれる交点の数と同じです。
　　　　　

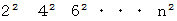
　 偶数マスのときは、 一辺の長さが２マスずつ大きくなるにつれ、 最短ルートの道のりは、 一辺の長さが２マスの正方形の場合から、 次のように増えていきます。 それは、正方形に含まれる交点の数よりも １ だけ大きくなっています。 なぜなら、 途中で１回通ったことのある交点を１回だけ通るという余分な移動をしているからです。 隣の交点に移動するとき、 その移動距離は １ マス です。
　　　　　

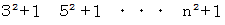
したがって、 答えは次のようになります。
　　　正方形の一辺の長さが 奇数マス のときは マス
　　　正方形の一辺の長さが 偶数マス のときは 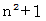マス