x 軸、 y 軸、 z 軸 からなる３次元直交座標系で表される空間に、 長さが １ の ３つの矢印 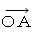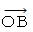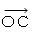， ， が 起点 Ｏ でそれぞれ直角にくっついた物体が存在します。
　 この物体を 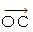を中心軸にして О から Ｃ に向かって時計回りに 度回転させることを ［Ｃ；］ と表すことにします。
　 また、 この物体を z 軸を中心軸にして z 軸の負の方から原点に向かって時計回りに 度回転させることを ［ z ；］ と表すことにします。

　 最初に、 Ａ，Ｂ，Ｃ をそれぞれ（ １，０，０ ），（ ０，１，０ ），（ ０，０，１ ）の座標で表される位置にセットします。 これをこの物体の元の姿勢とします。


（ 問題 １ ）

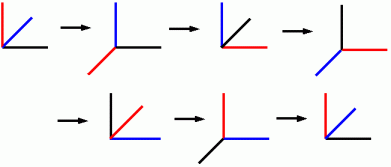
　 ［Ａ；90］ → ［Ｂ；90］ → ［Ｃ；90］ → ［Ａ；90］ → ［Ｂ；90］ →　・ ・ ・ ・　と繰り返して操作していったときに、 最低何回目の操作でこの物体は元の姿勢に戻りますか？

（ 問題 ２ ）

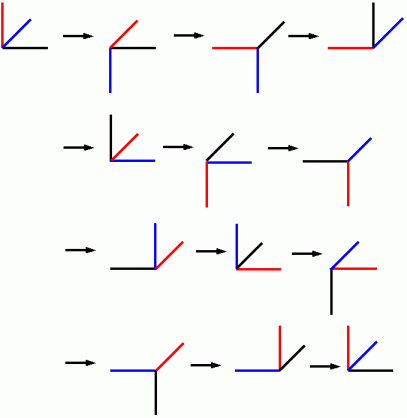
　 ［Ａ；−90］ → ［Ｂ；−90］ → ［Ｃ；−90］ → ［Ａ；−90］ → ［Ｂ；−90］ →　・ ・ ・ ・　と繰り返して操作していったときに、 最低何回目の操作でこの物体は元の姿勢に戻りますか？

（ 問題 ３ ）

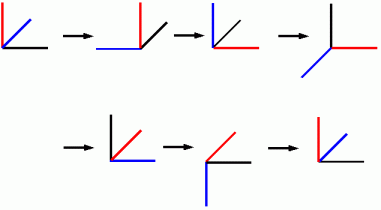
　 ［Ｃ；90］ → ［Ａ；90］ → ［Ｃ；90］ → ［Ａ；90］ → ［Ｃ；90］ →　・ ・ ・ ・　と繰り返して操作していったときに、 最低何回目の操作でこの物体は元の姿勢に戻りますか？

（ 問題 ４ ）

　 ［ z ；90］ → ［ x ；］ の２回の操作をしたところ、 Ａ，Ｂ，Ｃ はそれぞれ次の座標で表される位置に移動しました。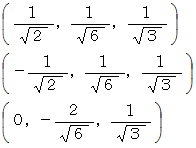
　　　　　　
の値を小数点以下を四捨五入して求めなさい。

（ 問題 １ の解答 ）

　　　答え ：　６回

　　　　　　　　　


（ 問題 ２ の解答 ）

　　　答え：　12 回

　　　　　　　　　


（ 問題 ３ の解答 ）

　　　答え ：　６回

　　　　　　　　　


（ 問題 ４ の解答 ）

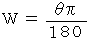　と置きます。
２回目の操作では、 を z 軸から y 軸の方向へ向かって 度回転させることになります。
この物体の最後の姿勢のときに、 次の式が成り立ちます。
　　　　　
　　　　　
　　　　　

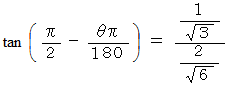
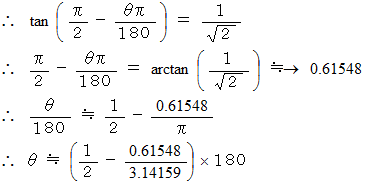
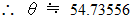
したがって、 答えは　55（ 度 ）になります。