再掲 ：
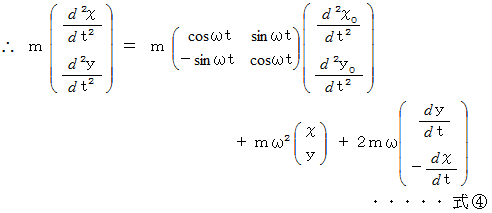
（２） 例題 １
-
反時計回りに角速度
で自転している等速自転座標系において、 
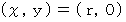の位置に静止している質量 
の質点Ｐ があります。 等速自転座標系における質点Ｐ の運動方程式は次のように表されるのは明確ですが、 これを式
から導いてみましょう。
静止座標系における質点Ｐ の存在する位置
は次のように表されます。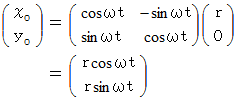
したがって、 次のようになります。
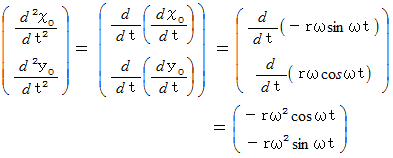
また、 次の式が成り立ちます。
これらを式
に代入しますと、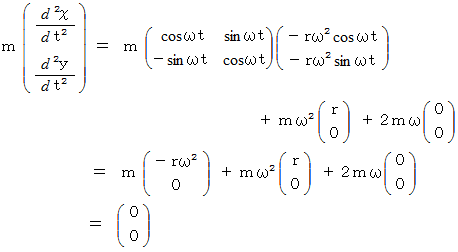
-
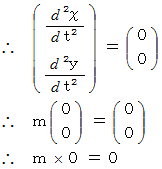
静止座標系において
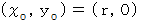の位置に静止している質量 の質点Ｐ があります。 これを、 反時計回りに角速度 で自転している等速自転座標系にいる観察者が観察した時の運動方程式を導いてみましょう。まずは、 普通の方法から。
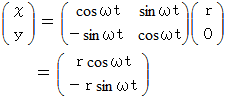
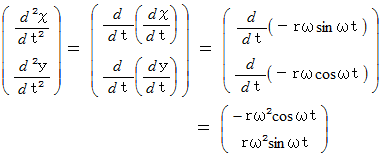
したがって、 答えは、 次のようになります。
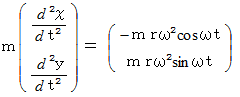
右辺は向心力になっており、 その大きさは
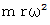になっています。次は、 式
を使って答えを求めてみましょう。明らかに静止座標系における質点Ｐ の加速度は
です。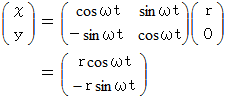
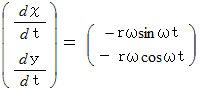
これらを式
に代入すると、 次のようになります。
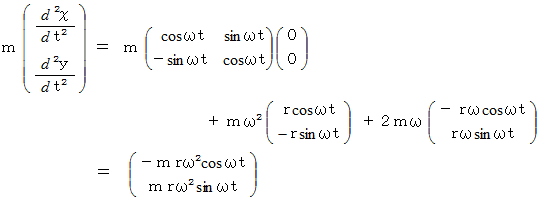
これが答えです。 遠心力 と コリオリの力 が加わって向心力になっています。物質に作用する向心力の向きは物質の位置ベクトルと逆向きです。
-
静止座標系において 時刻
のときに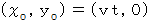 
の位置に存在し、 等速直線運動をしている質量 の質点Ｐ があります。 これを、 反時計回りに角速度 で自転している等速自転座標系にいる観察者が観察したときの、 質点Ｐ に作用する 遠心力 と コリオリの力 を求めてみましょう。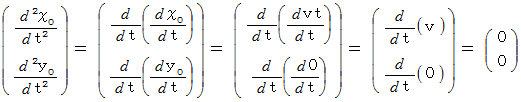
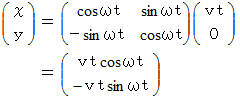
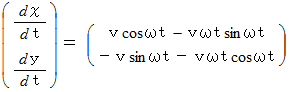
これらを式
に代入すると、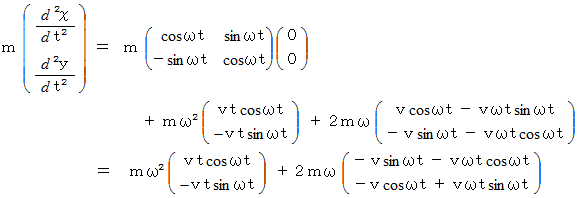
したがって、 遠心力は次のようになります。
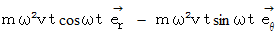
また、 コリオリの力は次のようになります。
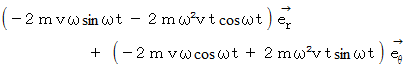
さて、
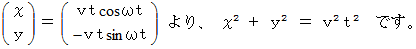
したがって、 等速自転座標系における質点Ｐ の軌道は、 原点から次第に曲率を大きくしていく螺旋になります。
この論文のトップへ戻る