【 問 題 １ 】

△ABC がある。
　　　
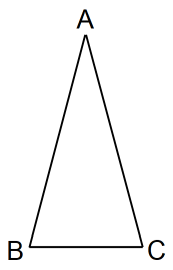
　　　　　　BC ＝ 1
　　　　　　AB ＝ AC
　　　　　　∠BAC ＝ 30°

辺ABの長さ と △ABCの面積 を求めよ。

【 解 答 】

　　　

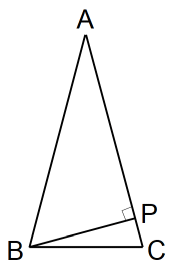
AB ＝ AC ＝ x とする。
△ABCの高さ ＝ h とする。

BP ＝ ABsin30°＝ x/2
△ABCの面積 ＝ x²/4
△ABCの面積 ＝ h/2
　　　よって、 h ＝ x²/2
ピタゴラスの定理より、 (1/2)² ＋ h² ＝ x²
よって、
　　　
　　　
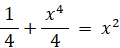
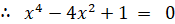
y ＝ x² と置くと、
　　　
　　　
　　　
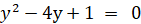
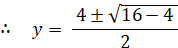
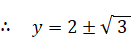
x² ＞ 1　より、
　　　
　　　
　　　
　　　
　　　
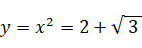
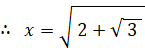
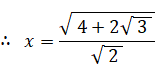
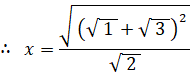
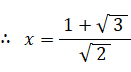
△ABCの面積は、
　　　

【 問 題 ２ 】

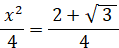
△ABC がある。
　　　
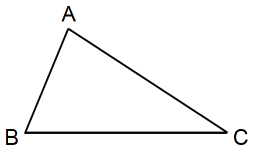
　　　　　　AB ＝ 3
　　　　　　AC ＝ 5
　　　　　　∠ABC ＝ ２×∠ACB

辺BCの長さを求めよ。

【 解 答 】

　　　

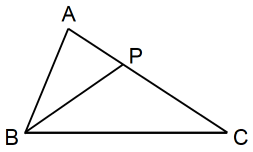
PB ＝ PC とする。
AP ＝ x 　BC ＝ y　と置く
△APB と △ABC は相似である。
AP：AB ＝ AB：AC　だから　x：3 ＝ 3：5
よって、x ＝ 9/5
したがって、 PB ＝ 5 − 9/5 ＝ 16/5
AB：BP ＝ AC：CB　だから　3：16/5 ＝ 5：y
よって、 y ＝ 16/3