２次元平面において２つの半直線が作る角の大きさを調べるときには、 どちらかの半直線を平行移動して端点と端点を重ねてから、 πラジアン以下の角度の方を測っていると思います。 しかし、 πラジアン以上の角度の方を測ってもいいと思います。 そこで、 この曖昧さを克服するために、 新しい角度の表現法を提案したいと思います。

　「 半直線Ａの半直線Ｂに対する角度 」 いう言い方をして、 その大きさを測るには、 どちらかの半直線を平行移動して端点と端点を重ねてから、 半直線Ｂをどれだけ反時計回りに回転すれば半直線Ａに重なるのかを調べ、 ０以上２π未満 ラジアン で表示します。

早速、 この角度の表現法を用いて、次の真の命題を証明してみましょう。

　命題 ：

　 ある四角形が 外接円を持つ四角形 に属するならば、 その四角形は 向かい合う角の和がπラジアンの四角形 に属する。
　　　　　

　その証明 ：

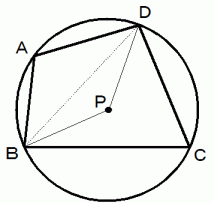
　　　ＡＤ　の　ＡＢ　に対する　角度　を　x ラジアン とする。
　　　ＣＢ　の　ＣＤ　に対する　角度　を　y ラジアン とする。
　　　ＰＢ　の　ＰＤ　に対する　角度　を　Ｑ ラジアン とする。
　　　ＰＤ　の　ＰＢ　に対する　角度　を　Ｗ ラジアン とする。

　　　中心角の大きさは円周角の大きさの２倍だから、
　　　　　　Ｗ　＝　２ x
　　　　　　Ｑ　＝　２ y
　　　よって、
　　　　　　２ x ＋ ２ y　＝　Ｗ ＋ Ｑ　＝　２π
　　　したがって、
　　　　　　 x ＋ y 　＝　π