1つの要素を無作為に抽出したときに、その要素がどれくらいの頻度である集合の要素であるか? というのが確率の基本です。そのためには、ベン図の各区域の中の要素の数がわかればよいのです。
例えば、2人の子どもがある家庭において、男の子と女の子の2人である確率:
-
( 第1子,第2子 ) = ( 男,男 ), ( 男,女 ), ( 女,男 ), ( 女,女 )
これらは、すべて独立事象であり、同様に確からしい。
集合A: 第1子が 男
集合B: 第2子が 男
全集合の要素の数: 4
集合A または 集合B の補集合 ( 女,女 )の数:1 ← ①
集合A かつ 集合Bの補集合 ( 男,女 )の数:1 ← ②
集合B かつ 集合Aの補集合 ( 女,男 )の数:1 ← ③
集合A かつ 集合B ( 男,男 )の数:1 ← ④
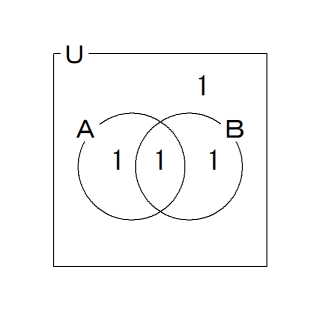
求めるもの: ② + ③ =→ 1+1 =→ 2
したがって、求める確率は 2÷4 =→ 0.5
 論理学 へ戻る
論理学 へ戻る