（１） 初項１ 公差１ の数列　　（ 三角数 ）

初項１ 公差１ の数列 ：　 1　 2　 3　 4　 5　 6
等差数列の和の数列 ：　 1　 3　 6　10　15　21

数列のｎ項目 ：　
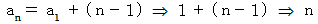
数列の漸化式 ：　

　　　　　　　　　　　　
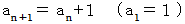
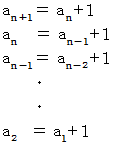
　　　　　　　　　辺々を加えると、
　　　　　　　　　　　　

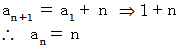
数列の和の数列のｎ項目 ：　

　　　　　

（２） 初項１ 公差２ の数列　　（ 四角数 ）

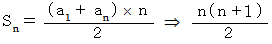
初項１ 公差２ の数列 ：　 1　 3　 5　 7　 9　11
等差数列の和の数列 ：　 1　 4　 9　16　25　36

数列のｎ項目 ：
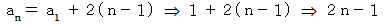
数列の漸化式 ：　

　　　　　　　　　　　　
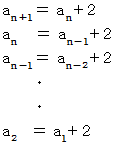
　　　　　　　　　辺々を加えると、
　　　　　　　　　　　　

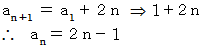
数列の和の数列のｎ項目 ：　

　　　　　

（３） 初項１ 公差３ の数列

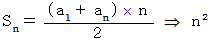
初項１ 公差３ の数列 ：　 1　 4　 7　10　13　16
等差数列の和の数列 ：　 1　 5　12　22　35　51

数列のｎ項目 ：　
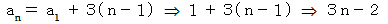
数列の漸化式 ：　

　　　　　　　　　　　　
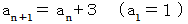
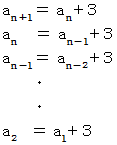
　　　　　　　　　辺々を加えると、
　　　　　　　　　　　　

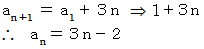
数列の和の数列のｎ項目 ：　

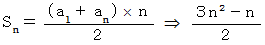
（４） 初項１ 公差 の数列

数列のｎ項目 ：　
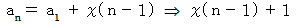
数列の漸化式 ：　

　　　　　　　　　　　　
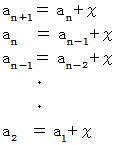
　　　　　　　　　辺々を加えると、
　　　　　　　　　　　　

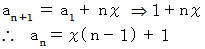
数列の和の数列のｎ項目 ：　


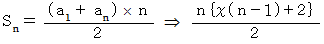
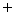
　 初項１ 公差 の等差数列の和の数列は 「 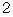（）角数 」 と言われます。 それは、 初項１ 公差 の等差数列の和の数列を碁石を並べて表現するときに、 各項目が全体として正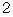（）角形になるように並べて行くと見やすくなるからです。

　 初項１ 公差４ の等差数列の和の数列のｎ項目は 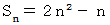です。 したがって、 ６角数は次のようになります。

　　　６角数 ：　１　６　15　28　・ ・ ・ ・

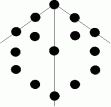
　　　　　　　間違った並べ方 （ 初項１ 公差６ の等差数列になっています ）
　　　　　　　　　　　　　　　　　　　　

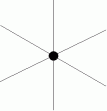
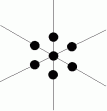
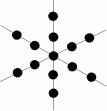
　　　　　　　正しい並べ方