２つの周期 ２π の周期関数の内積は次のように表されます。
　　　　
　２つの関数が共に三角関数であるとき、２つの関数は直交します。直交するとは、内積が 0 になるということです。

　このことを確かめるため、次の２つの三角関数を例にとってその内積をとりましょう。
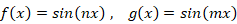　　　　　　ただし、n ≠ m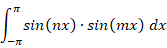
　　　
　　　　　　　　　
　　　　　　　　　
　　　　　　　　　
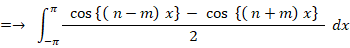
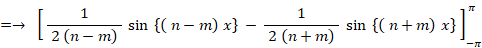
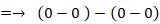
　　　　　　　　　＝→　0

　というわけで、２つの三角関数は直交していることが分かりました。三角関数は直交しているというのは、位相が90°異なっているというのとは違います。

　では、三角関数の自分自身の内積はどうなるでしょうか？　それは先ほどの２つの関数の内積の n ＝ m の場合を考えると分かります。
　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
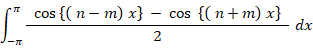
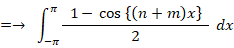
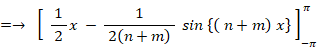
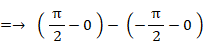
　　　　　　　　　　　　　＝→　π

　というわけで、三角関数の自分自身の内積は π になることが分かりました。ということは、三角関数の大きさは ルート(π) であるということでしょうか？

　※　参考：
　　　　大学生のための数学 ＞ 線形代数学 ＞ ２つの関数の正規相関関係
　　　　大学生のための数学 ＞ 解析学 ＞ フーリエ級数展開
　　　　大学生のための数学 ＞ 十進BASIC ＞ 十進BASIC ＿算数 ＞ sin x と cos x の内積
　　　　大学生のための数学 ＞ その他の数学 ＞ Desmosで畳み込み