次のような条件を満たす関数にはどんなものがあるか考えてみましょう。










































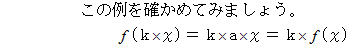
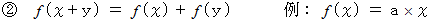
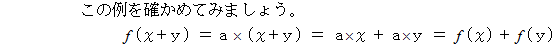
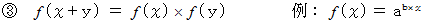
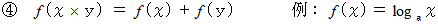
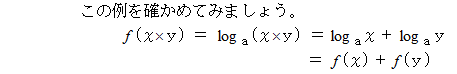
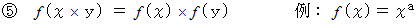
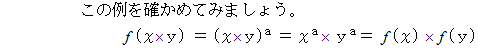
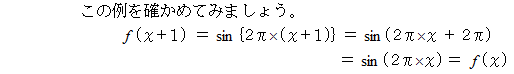
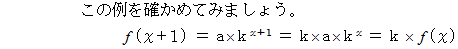
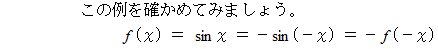
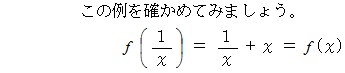
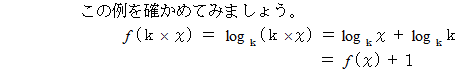
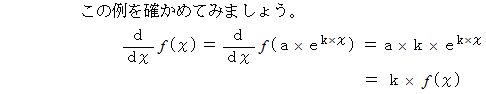
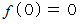　 を満たす の１次式で表される関数のように、 と を同時に満たす関数は、「 線形変換 」と言われます。 これは「 線形変換を担う関数 」と言ってもいいと思います。 ベクトルとベクトルとを対応させる関数も「 線形変換 」です。 それはテンソルによって担われます。

　 は、 周期関数と言われます。

　 は 等差級数 を、 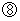は 等比級数 を連想させます。

　 は、 グラフにすると左右対称です。 は、 上下逆にしても同じグラフです。

　 は、 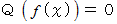という、 ある関数 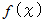についての関数式になっています。 関数の関数を取り扱った式です。 この式が成り立っているとき、 その関数式は についての恒等式になっています。 つまり、 変数 がどんな値を取ろうとも、 その式は成立します。
　　　どんな関数についても、 次の関数式は成り立ちます。
　　　　　　　
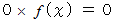
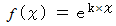　　　 という関数については、 次の関数式が成り立ちます。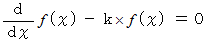
　　　　　　　
　　　　　　　　　　　この関数式は、 関数が 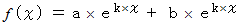のときにも
　　　　　　　　　　成り立ちます。 このように関数式を満たす基本的な関数が見つかれば、
　　　　　　　　　　それを線形結合させることによって、 この関数を満たすような関数が次々
　　　　　　　　　　に見つかるような「 関数の関数式 」のことを、「 線形方程式 」と言います。