(1) 論理学における真偽表
-
「 吾輩は猫である。」 「 吾輩は犬である。」 「 吾輩は獣である。」
-
A
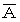








-
A
B
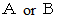












-
A
B
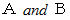












-
A
B
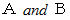
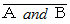
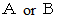
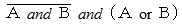
























このような文章たちを命題といいます。 命題には本当のことを言ったものと嘘を言ったものとがあり、 前者を真 (
 ) の命題、 後者を偽 (
) の命題、 後者を偽 (  ) の命題といいます。 また、 「 吾輩は猫ではない。」 という命題を 「 吾輩は猫である。」 という命題の否定といいます。
) の命題といいます。 また、 「 吾輩は猫ではない。」 という命題を 「 吾輩は猫である。」 という命題の否定といいます。2つの命題 A と B があります。 A が真の命題のとき、 A の否定 (
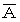 ) は偽の命題です。 A も B も真の命題のとき、 A かつ B (
) は偽の命題です。 A も B も真の命題のとき、 A かつ B ( 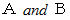 ) は真であるといい、 A も B も偽の命題のとき、 A または B (
) は真であるといい、 A も B も偽の命題のとき、 A または B ( 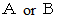 ) は偽であるといいます。
) は偽であるといいます。これらの複合命題の真偽判定を、 さまざまなケースについて漏れなく表にまとめたものを真偽表といいます。
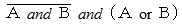 は、 「 2つの命題 A と B の 真 と 偽 は異なる。」 という命題の真偽判定をしているので、 Difference referee と言うことにし、 次のように表すことにします。
は、 「 2つの命題 A と B の 真 と 偽 は異なる。」 という命題の真偽判定をしているので、 Difference referee と言うことにし、 次のように表すことにします。Difference referee ( A, B )
また、 それぞれの複合命題の真偽判定を、 次のように言って、 関数のように表現することにします。
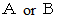 : Lenient umpire Or ( A, B )
: Lenient umpire Or ( A, B )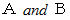 : Strict umpire And ( A, B )
: Strict umpire And ( A, B )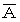 : Negative umpire Not ( A )
: Negative umpire Not ( A )-
命題が真のときは 「 命題スイッチ 」 が ON で、 回路の一部に電流が流れるとします。 複合命題が真のときは 「 論理回路 」 に電流が流れるとします。 「 論理回路 」 は、 複数の 「 命題スイッチ 」 を入り口として、 複数の 「 内付けリレースイッチ 」 を導線で繋げたものです。
「 命題スイッチ 」 は 「 外付け初期設定スイッチ 」 のことでもあり、 これを担うのはいわゆる 「 スイッチ 」 で、 人が操作します。 「 内付けリレースイッチ 」 を担うのはトランジスタです。 複数の 「 命題スイッチ 」 の ON・OFF の直接的あるいは間接的結果として、 トランジスタに電流が流れ出す (
 ) と、 トランジスタは スイッチON の状態になり、 別の電流が流れるのをストップさせていた今までとは逆に、 その電流を流すようになります (
) と、 トランジスタは スイッチON の状態になり、 別の電流が流れるのをストップさせていた今までとは逆に、 その電流を流すようになります ( 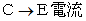 )。 トランジスタは、 P型半導体 を N型半導体 でサンドイッチにしたもので、 エミッタ ( E ) ・ ベース ( B ) ・ コレクタ ( C ) と呼ばれる端子を持ちます。 ベース端子は、 真ん中のP型半導体に繋がっています。 論理回路を構成するトランジスタの一部に電流が流れたとしても、 論理回路の出口のところで電流が流れていなければ、 その論理回路には電流が流れていないと見なされ、 複合命題は偽であると判断されます。
)。 トランジスタは、 P型半導体 を N型半導体 でサンドイッチにしたもので、 エミッタ ( E ) ・ ベース ( B ) ・ コレクタ ( C ) と呼ばれる端子を持ちます。 ベース端子は、 真ん中のP型半導体に繋がっています。 論理回路を構成するトランジスタの一部に電流が流れたとしても、 論理回路の出口のところで電流が流れていなければ、 その論理回路には電流が流れていないと見なされ、 複合命題は偽であると判断されます。 Lenient umpire : Or ( A, B ) OR回路 ( 基本論理回路 その1 )
Lenient umpire : Or ( A, B ) OR回路 ( 基本論理回路 その1 )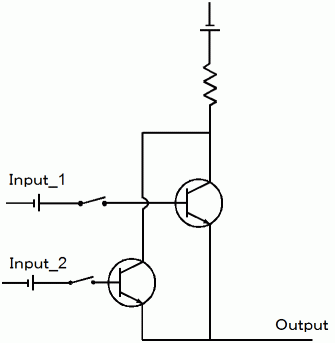
 Strict umpire : And ( A, B ) AND回路 ( 基本論理回路 その2 )
Strict umpire : And ( A, B ) AND回路 ( 基本論理回路 その2 )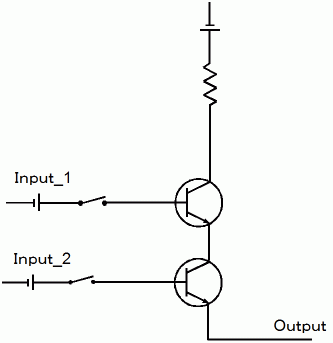
 AND回路は、 N型半導体 と P型半導体 を接合した
AND回路は、 N型半導体 と P型半導体 を接合したダイオードを2個使って作ることもできます。
 Negative umpire : Not ( A ) NOT回路 ( 基本論理回路 その3 )
Negative umpire : Not ( A ) NOT回路 ( 基本論理回路 その3 )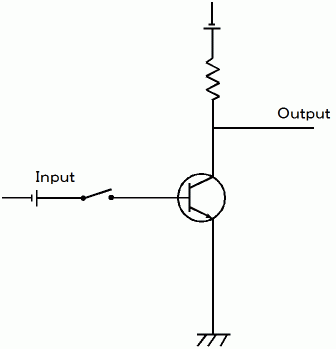
 Difference referee
Difference referee 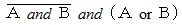 ( 複合論理回路の例 )
( 複合論理回路の例 )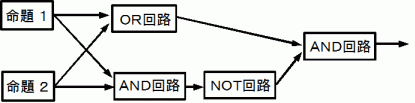
 プログラミング へ戻る
プログラミング へ戻る