【 問 題 】

　　　
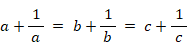
上式が成り立つとき、 a，b，c のうち少なくとも２つの値は一致することを証明せよ。

【 解 答 】

仮説：　a，b，c はすべて異なる数であると仮定する。

与式を次のように置く。
　　　
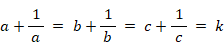
すると、次の３つの式が成り立つ。
　　a² − k a ＋ 1　＝　0
　　b² − k b ＋ 1　＝　0
　　c² − k c ＋ 1　＝　0
ということは、 a，b，c は すべて　x² − k x ＋ 1　＝　0　の解であるということである。
２次方程式の解の数は最高２個までなので、仮説と矛盾する。
よって、 a，b，c のうち少なくとも２つの値は一致する。