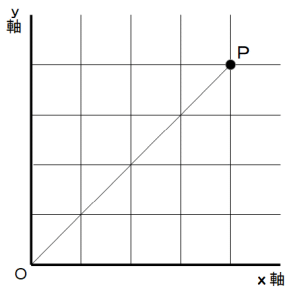
格子を通って最短距離で原点から点Ｐ（ ４，４ ） に至る経路は何通りあるでしょうか？
　　　１ ：　右に１つ進む
　　　２ ：　上に１つ進む
例えば、
　　　１ １ １ １ ２ ２ ２ ２
　　　１ ２ １ ２ １ ２ １ ２
　　　２ ２ １ ２ １ ２ ２ １　　など

　 ということは、 ８か所のうちから４か所の組み合わせを選ぶ場合の数であることに気づきます。 したがって、 答えは次のようになります。
　　　　　


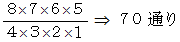
　 では、 原点 と 点Ｐ とを結ぶ線分よりも y 軸に近づかないという条件を加えると、 何通りになるでしょうか？　これを解くために、 次のような十進BASIC のプログラムを作って実行すると、 14通りであることが解ります。

　 では、 点Ｐ（ n，n ） の場合、 原点 と 点Ｐ とを結ぶ線分よりも y 軸に近づかない最短距離の経路は何通りになるでしょうか？　これは難しいので、 答えをお教えしましょう。
　　　　　
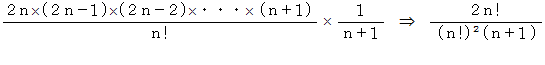
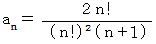と置くと、 次のようになります。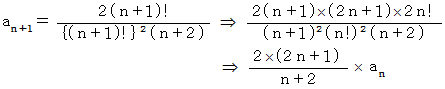
　　　　　
　　　　　

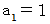
　 したがって、 次のような十進BASIC のプログラムを組んで実行すると、 n が大きくても短時間で具体的な値を知ることができます。

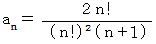　で表される数列は、 カタラン数列と言われています。
　　1　　2　　5　　14　　42　　132　　429　　1430　　4862　　16796　・ ・ ・

カタラン数列の第５項を求める問題 ：

　 １ と ０ の数字が５個ずつあります。 これらを左から順番に10個並べていきます。 途中で ０ の個数が １ の個数を上まらないようにすることが条件です。 何通りあるでしょうか？

　 ０ からスタートします。 コインを投げて表が出れば １ 進み、 裏が出れば １ 戻ります。 −１ になることなく10回目で ０ に戻るのは、 何通りあるでしょうか？

　※ 参照： 大学生のための数学 ＞ 十進BASIC ＞ 十進BASIC＿算数 ＞ カタラン数は場合の数