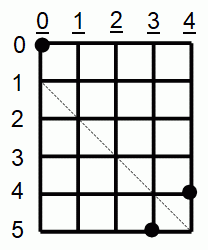
A : 点( 0 , 0 ) から 点( 4 , 4 ) まで 線上を通り 遠回りせずに行く。
B : 点( 1 , 0 ) かつ 点( 2 , 1 ) かつ 点( 3 , 2 ) かつ 点( 4 , 3 ) を通らない。
C : 点( 1 , 0 ) または 点( 2 , 1 ) または 点( 3 , 2 ) または 点( 4 , 3 ) を通る。
D : 点( 0 , 0 ) から 点( 5 , 3 ) まで 線上を通り 遠回りせずに行く。
A かつ B の場合の数を求めるには、 A の場合の数 から A かつ C の場合の数 を引けばよい。
A かつ C の場合の数は、 D の場合の数に等しい。
なぜなら、 D の場合いのルートを 点( 1 , 0 ) と 点( 5 , 4 ) とを結ぶ線分で折り返して重ねると、 A かつ C の場合のルートに必ずなるからです。
A の場合の数 : 8C4 =→ 70
A かつ C の場合の数 : 8C3 =→ 56
したがって、 A かつ B の場合の数 = 70 − 56 =→ 14 ( とおり )
以上、 カタラン数列の第4項の値を求めたのですが、 同様にして、 カタラン数列の第n項の値
 は次のようになります。
は次のようになります。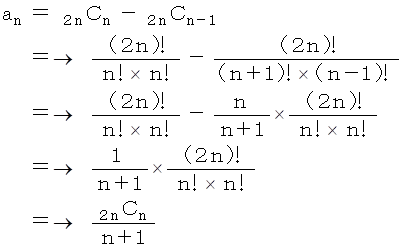
* 参考 : 十進BASIC > 十進BASIC_算数 > カタラン数は場合の数
 数理論 へ戻る
数理論 へ戻る