(1) 円 と 楕円 の方程式
-
図 1
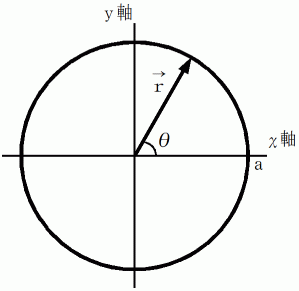
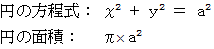
円の方程式は、 ベクトル
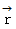 を用いて、 次のようにも表すことができます。
を用いて、 次のようにも表すことができます。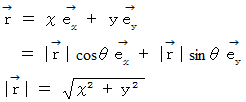
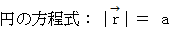
図 2
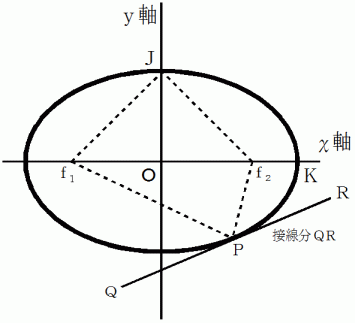
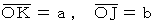
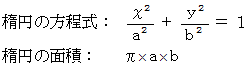

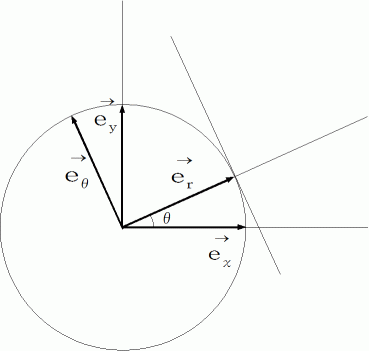
楕円の方程式は、 図 3 の ベクトル
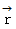 を用いて、 次のようにも表すことができます。
を用いて、 次のようにも表すことができます。図 3
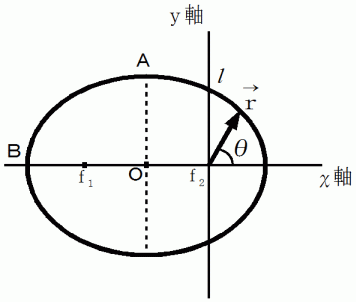
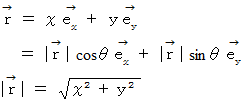
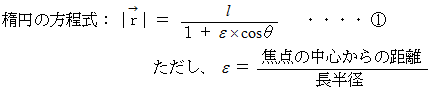
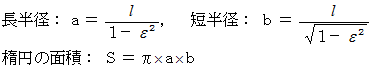
 より、
より、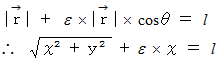
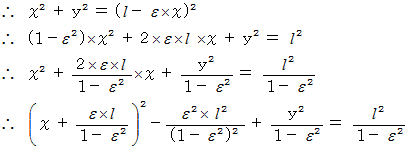
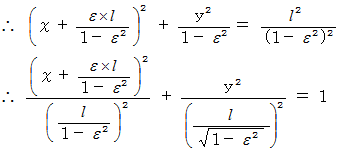
これは、
 が、 次のような楕円を表す式であることを示しています。
が、 次のような楕円を表す式であることを示しています。
-
はじめに、 角速度
 と 速度 との関係は次のようになっています。
と 速度 との関係は次のようになっています。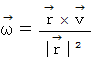
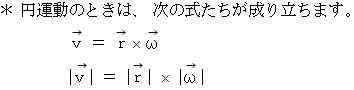
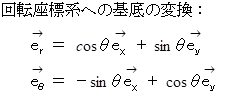
まず、 円運動の速度を求めてみましょう。 もう一度、 図 1を見てください。
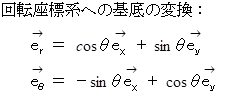
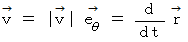
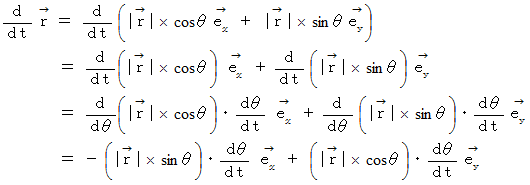
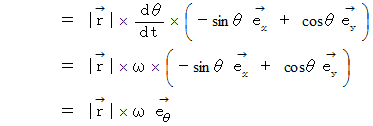
したがって、次の式が成り立ちます。
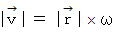


次に、 円運動の加速度を求めてみましょう。
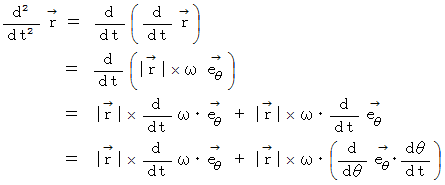
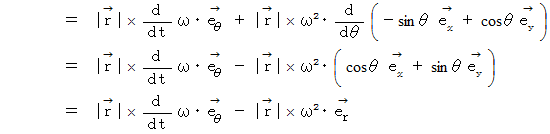
この式の両辺に、 質量
 をかけると、 運動方程式になります。
をかけると、 運動方程式になります。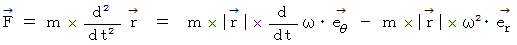
接線力 :
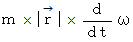
向心力 :
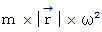


 を
を  に代入すると、 次の式になります。
に代入すると、 次の式になります。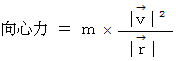
等速円運動のときは、
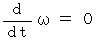 ですから、 接線力は
ですから、 接線力は  になります。
になります。-
等運動量変位( 運動量が一定の移動 )とは、 等速直線運動のことです。 等速直線運動は、力 が作用しない移動です。 等運動量変位を式で表すと次のようになります。
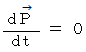
したがって、 次のように展開されます。
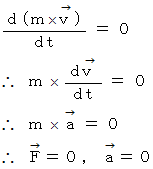
では、 等運動量モーメント変位( 運動量モーメントが一定の移動 )とはどんな移動でしょうか? 運動量モーメントは次のような式で表されます。
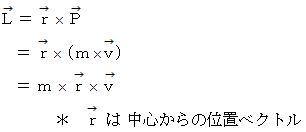
さて、 面積速度 というのがあります。 ケプラーの第2法則には、 楕円運動における等面積速度変位が登場しますが、 等面積速度変位とは等運動量モーメント変位のことです。 というのは、 面積速度は次の式で表されるからです。
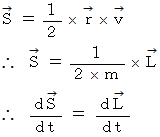
また、 面積速度は次のようなスカラーで表されることもあります。 ただし、 この式には、
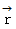 と
と 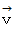 が直角であるという 微小近似が隠されています。
が直角であるという 微小近似が隠されています。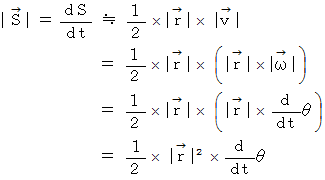
 力学 へ戻る
力学 へ戻る