(4) 曲線運動の 速度 と 加速度 の回転座標系への座標変換
-
曲線運動の 速度 と 加速度 の回転座標系への座標変換は、それぞれ次のようになります。
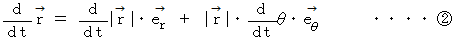
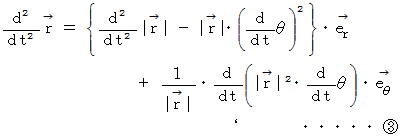
図4
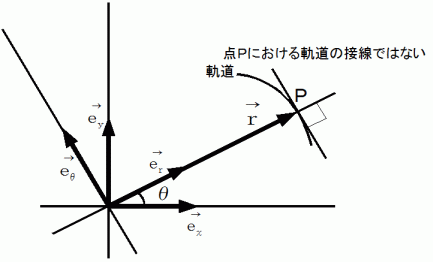
回転座標系への座標変換における基底の変換:
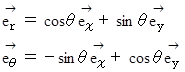
これから、曲線運動における 速度 と 加速度 の回転座標系への座標変換を導いてみましょう。
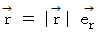
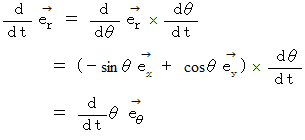
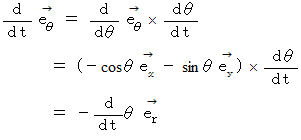
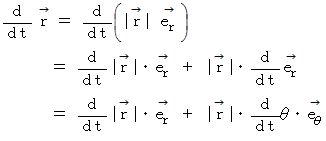
こうして、
 が導かれました。
が導かれました。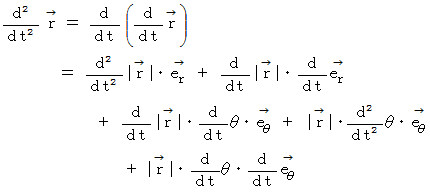
この式に、
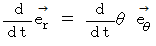 と
と 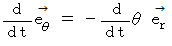 を代入すると、
を代入すると、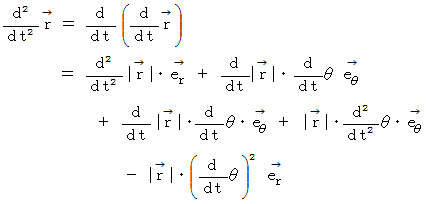
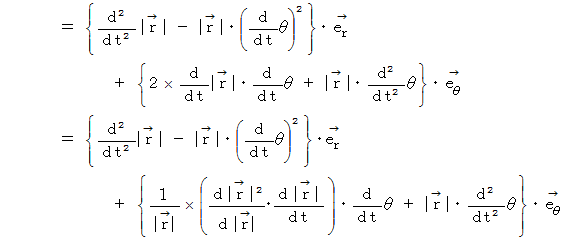
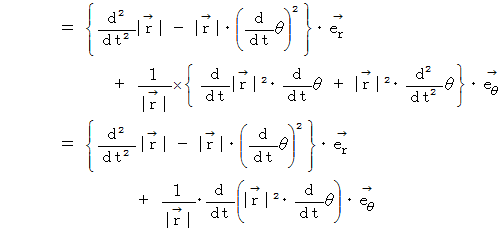
こうして、
 が導かれました。
が導かれました。-
ケプラーの法則とは、一言で言うと、「 惑星は太陽を焦点の1つとする等角運動量的楕円運動をしている。」という法則です。これは、ケプラーの第1&第2法則です。
角運動量が一定ですから、面積速度が一定です。 図3 でいうと、それは次のように書くことができます。
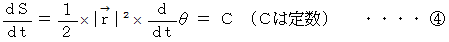
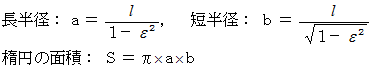
周期を
 とすると、
とすると、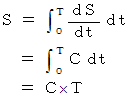
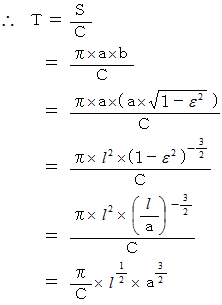
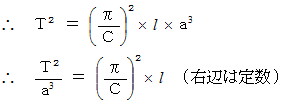
これは、ケプラーの第3法則です。ケプラーの第3法則とは、「 公転周期の2乗は、 長半径の3乗に比例する。」というものです。
 より、
より、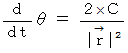
これを
 に代入すると、
に代入すると、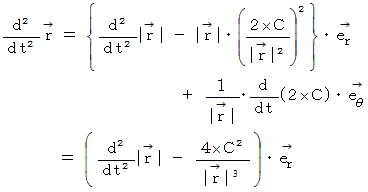
この両辺に
 をかけると、 運動方程式になります。
をかけると、 運動方程式になります。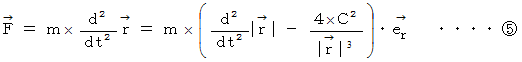
ところで、
 より次の式が成り立ちます。
より次の式が成り立ちます。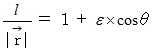
両辺を
 で微分すると、
で微分すると、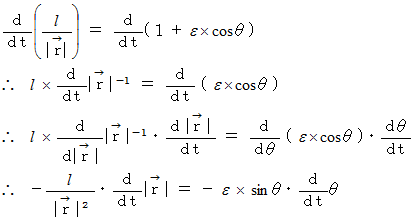
ここで、
 より、
より、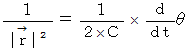
これを代入すると、
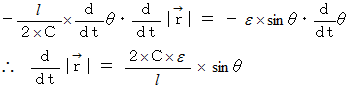
両辺を
 で微分すると、
で微分すると、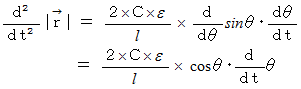
ここで、
 より、
より、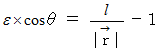
これを代入すると、
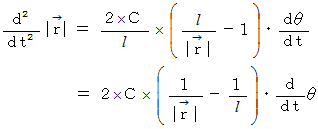
ここで
 より、
より、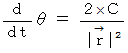
これを代入すると、
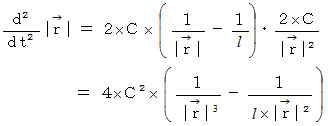
これを
 に代入すると、
に代入すると、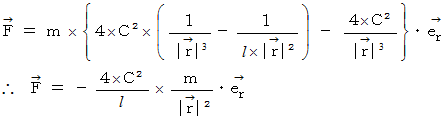
作用反作用の力を考慮すると、 次のような式が成り立つと言えます。
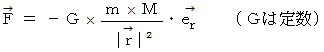
これが、 万有引力の法則です。
 次のページへ進む
次のページへ進む