月や地球の公転は円軌道と考えて差し支えありませんが、 正確にいうと楕円軌道です。 では、 どれくらい円から歪んだ楕円なのでしょうか? それをイメージするためには次のようなデーターを用います。
月の公転軌道における遠地点距離と近地点距離の比 ≒ 1.116
地球の公転軌道における遠日点距離と近日点距離の比 ≒ 1.034
楕円の方程式 :
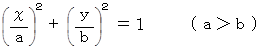
この楕円は中心が原点にあり、 長軸はχ軸上、 短軸はy軸上にある。
長軸半径は a 、 短軸半径は b 。
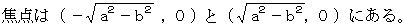
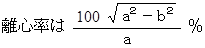
まず、 月と太陽の公転軌道における長軸と短軸の長さの比を比べてみましょう。
近点距離を 1 、 遠点距離を L とします。
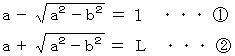
 と
と  を辺々加えることにより、
を辺々加えることにより、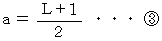
 より
より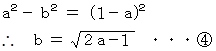
 と
と  より
より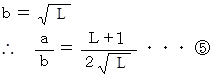
 に L = 1.116 と L = 1.034 を代入して、
に L = 1.116 と L = 1.034 を代入して、月の公転軌道における長軸と短軸の長さの比 ≒ 1.0015
地球の公転軌道における長軸と短軸の長さの比 ≒ 1.00014
これを見ると、 月や地球の公転軌道はほぼ円であると言えますね。
最後に、 楕円の円からの歪を表す指標である 離心率 で比べてみましょう。
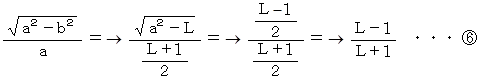
 に L = 1.116 と L = 1.034 を代入して、
に L = 1.116 と L = 1.034 を代入して、月の公転軌道における離心率 ≒ 5.5 %
地球の公転軌道における離心率 ≒ 1.67 %
今回のまとめとして、 月や地球の公転軌道はほぼ円であると言えるが、 正確に言うと楕円であり、 その円からの歪の程度は月の公転軌道が地球の公転軌道の約3倍である、 と言えます。
 天文学と物理学 へ戻る
天文学と物理学 へ戻る