次の (1) のように、 奇数列 と 偶数列 とは異なる法則によって決められているのですが、 それらを1つに統合すると、 隣合う数たちにはある関係性が成り立っています。
(1) ちょっと複雑な数列 その1
 は
は  以上の整数
以上の整数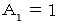
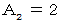
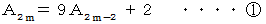
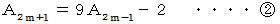
上記のとき、 数列
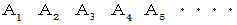 は、 次のようになります。
は、 次のようになります。1 2 7 20 61 182 547 1640 ・ ・ ・ ・
(2) ちょっと複雑な数列 その2
 は
は  以上の整数
以上の整数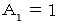
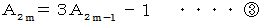
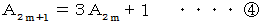
上記のとき、 数列
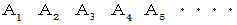 は、 次のようになります。
は、 次のようになります。1 2 7 20 61 182 547 1640 ・ ・ ・ ・
(3) ちょっと複雑な数列 その3
 は
は  以上の整数
以上の整数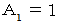
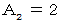
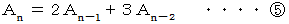
上記のとき、 数列
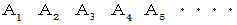 は、 次のようになります。
は、 次のようになります。1 2 7 20 61 182 547 1640 ・ ・ ・ ・
(4) ちょっと複雑な数列 その4
 は
は  以上の整数
以上の整数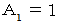
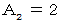
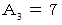
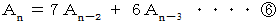
上記のとき、 数列
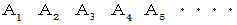 は、 次のようになります。
は、 次のようになります。1 2 7 20 61 182 547 1640 ・ ・ ・ ・
以上の (1) から (4) の4つの数列は、 すべて同じです。 なぜでしょうか?
まず、 (2) から (3) を導きます。
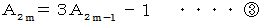
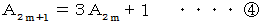
 より、
より、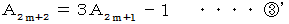
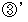 と
と  を 辺々加えると、
を 辺々加えると、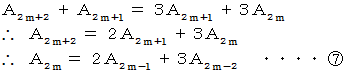
 と
と  を 辺々加えると、
を 辺々加えると、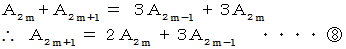
 と
と  より、 これらの式たちは、
より、 これらの式たちは、 は
は  以上の整数 とすると、
以上の整数 とすると、  の式1つで表すことができることが解ります。
の式1つで表すことができることが解ります。次に、 (2) から (1) を導きます。
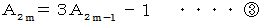
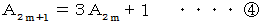
 を
を  に代入すると、
に代入すると、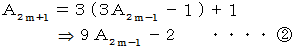
 より、
より、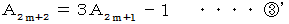
 を
を 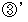 に代入すると、
に代入すると、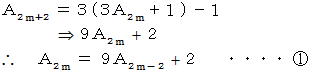
その次に、 (3) から (4) を導きます。
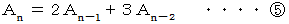
 は
は  以上の整数とすると、
以上の整数とすると、  は次のようにも表すことができます。
は次のようにも表すことができます。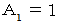
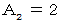
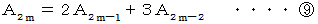
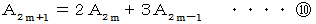
 より、
より、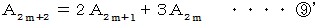
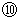 より、
より、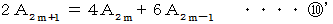
 と
と  を辺々加えると、
を辺々加えると、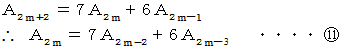
 より、
より、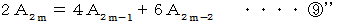
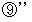 と
と  を辺々加えると、
を辺々加えると、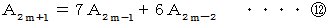
 と
と  より、 これらの式たちは、
より、 これらの式たちは、 は
は  以上の整数 とすると、
以上の整数 とすると、  の式1つで表すことができることが解ります。
の式1つで表すことができることが解ります。(1) から (4) の数列が本当に同じものなのかどうか、 十進BASIC のプログラムで確かめてみました。
 数理論 へ戻る
数理論 へ戻る