静止摩擦力は発生しますが運動摩擦力が全く生じない円盤が反時計回りに等速自転しています。円盤の中心にあなた (Ａ) が乗っていて円盤の縁にあなたの友達 (Ｂ) が乗っています。あなたやお友達は円盤と同じ角速度で自転しています。あなたは友達に向けてボールを転がしますが、円盤が自転しているためにボールはあなたから見て友達よりも右側に大きくそれていきます。下の図の青色は、あなたの座標系におけるボールの軌跡を模式的に表したものです。あなたの座標系（等速自転座標系）では、ボールには、みかけの力であるところの遠心力とコリオリの力が作用します。それらは向きを変えながら次第に大きくなっていきます。

　　　　　　　　　　
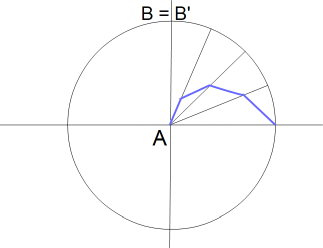
　これを円盤の周囲から見ている人からすると、ボールはまっすぐに転がって友達の元いた場所に届きます。
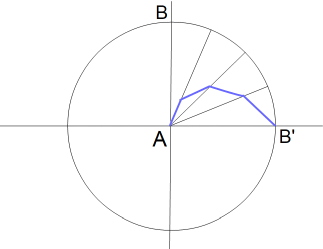
　今度は、友達があなたに向けてボールを転がしますが、円盤が自転しているためにボールは友達から見てあなたよりも右側に大きくそれていきます。これを円盤の周囲から見ている人からすると、ボールは最初から円盤の中心よりも右側に向けて放たれてまっすぐに転がっていきます。垂直方向の２つの速度の合成が起きるからです。

　静止摩擦力は発生しますが運動摩擦力が全く生じない１階のフロアーの上でＡ君とＢ君の２人がボールを転がしてキャッチボールをしています。それを透明なガラスでできた２階のフロアーから観察者は見ています。椅子に座って反時計回りに等速自転しながら。これは上記のシチュエーションと全く同じではありません。Ｂ君にもコリオリの力が働き、それは向心力となりＢ君は等速円運動をするからです。Ｂ君にも遠心力が働きますが、それはコリオリの力にはとうてい及びません。

　　　　　　　　　　
　※ 参考： 力学 ＞ 等速自転座標系の運動方程式（ 遠心力やコリオリの力の正体 ） の（３）例題２

　もし、１階のフロアーが観察者と同じ角速度で回転したら、どうなるでしょうか？　それは文頭で述べたシチュエーション全くと同じになります。

　円盤が反時計回りに等速自転しています。円盤の中心にあなたが乗っていて円盤の縁にあなたの友達が乗っています。あなたの所にいたヤモリがお友達に向かって全速力で円盤の上を手足の吸盤を使って移動しました。出発と同時に閉眼して。ヤモリは進行方向に対して右向きのコリオリの力を受け、次第に少しずつではありますが目指す所よりも右側へ変位していきます。
　あなたやヤモリにとっては円盤は静止していますが、円盤の真上から見ている人にとっては、ヤモリが出発して円盤の縁へ向かうにつれヤモリが接触する円盤の部分の回転速度が大きくなっています。（ 角速度は一定ですが ） ヤモリは移動するたびに回転速度が次の円盤の接触部分よりわずかに遅いために、円盤がヤモリに対して加速的変速度運動をすることになり、慣性の法則によりヤモリはその場に取り残されようとするのです。円盤の真上から見ている人にとっては、そういった慣性力が作用していることになります。

　地球が角速度の大きさ ω rad/s で反時計回りに等速自転しているとします。赤道上に存在する人が 0 時 に出発して、速さ v km/s でまっすぐに北極点を目指します。t 秒後に彼は v sin ωt km/s の速さで地軸に近づいていることになります。

　半径10mの透明な球形カプセルの中心であなたは反時計回りに等速自転しています。球形カプセルはあなたと同じ角速度で自転しています。「自転するカプセルの中心にいてカプセルと同じ角速度で自転するあなた」というのは、「自転する円盤の中心で円盤と同じ角速度で自転するあなた」の３次元バージョンです。
　カプセルの天頂にヤモリがいます。その後ヤモリは全速力で最短ルートを通ることを目指してカプセルの赤道に向かいます。ヤモリは出発と同時に閉眼します。ヤモリが天頂から赤道に移動する間、ヤモリは少しずつ右側にずれていきます。それは、あなたやヤモリにとって、ヤモリに見かけの力であるコリオリの力が作用するからです。また、あなたやヤモリにとっては、ヤモリには、地軸に向かう向心力とその反対方向に向かう遠心力も作用しています。
　あなたやヤモリにとってカプセルは静止していますが、カプセルの天頂よりもずっと高い所にいる人が見ると、ヤモリは赤道に向かいながら慣性力を受けて少しずつ右側にずれていきます。なぜなら、ヤモリが出発して赤道へ向かうにつれヤモリが接触するカプセルの部分の回転速度が大きくなっていくからです。（ 角速度は一定ですが ） ヤモリは移動するたびに回転速度が次のカプセルの接触部分よりわずかに遅いために、カプセルがヤモリに対して加速的変速度運動をすることになり、慣性の法則によりヤモリはその場に取り残されようとするのです。カプセルの天頂よりもずっと高い所にいる人にとっては、そういった慣性力が作用していることになります。
　この思考実験は、台風の渦のしくみを知るために有用です。

　半径10mの透明な球形カプセルの中心であなたは反時計回りに等速自転しています。球形カプセルは自転していません。
　カプセルの天頂にヤモリがいます。その後ヤモリは全速力で最短ルートを通ることを目指してカプセルの赤道に向かいます。ヤモリは出発と同時に閉眼します。ヤモリが天頂から赤道に移動する間、あなたにとってヤモリは赤道に向かいながらあなたの自転の角速度と同じ大きさの角速度で時計回りにあなたの自転軸の回りを公転します。ということは、あなたにとってヤモリは公転速度 ( 公転角速度は一定ですが ) を次第に大きくしながら赤道に向かいます。このヤモリの移動を司るのが遠心力とコリオリの力です。コリオリの力は、あなたにとってのヤモリの移動速度 に あなたの自転の角速度 を外積させて得られるベクトルの方向を向きます。したがって、その大きさは出発点ほど大きく、赤道近くになるとほぼ０になります。
　この光景をカプセルの天頂よりもずっと高い所にいる人が見るとどうなるでしょう？ 　ヤモリは何も力を受けないでまっすぐに進みます。ただし、縁に向かうスピードは最初は速いのですが、次第にそのスピードを落としていきます。