底面が１×１の正方向で高さが２の直方体があります。
底面のうちの１つの頂点を点Ａとします。
「 点Ａから面上を移動して行ける所で、最も遠い所はどこでしょうか？」と問えば、まず次のような答えが返ってくるでしょう。
「 それは、点Ａから対角線の引ける頂点Ｂです。なぜなら、点Ｂは点Ａから最も空間的に遠い所にあるからです。」
しかし、それは間違いであり、下図の点Ｐが正解です。

　　　

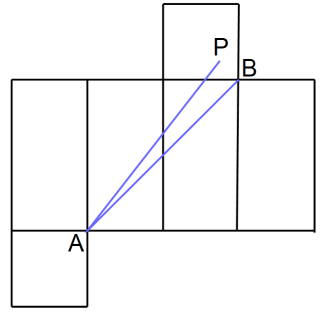
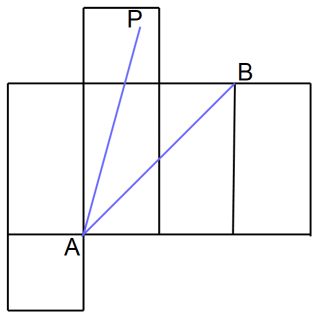
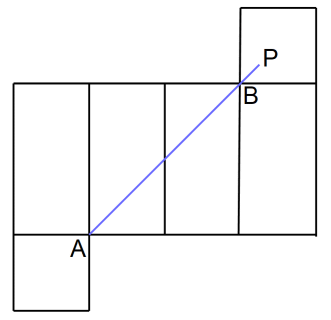
直方体の展開図を描いて、２点を結ぶ線分が最短距離です。
その最短距離が全ての展開図で等しい点のうち最短距離が最も長い点が、最も遠い点なのです。