（ 問 題 ）

　 単位格子が描かれている２次元直交座標の図があります。
そこに 点（ ０，０ ）， 点（ ２ｎ，０ ）， 点（ ｎ，２ｎ ）、 ただし ｎ は自然数、 を頂点とする三角形を描きます。 このとき、 すべての ｎ についてピックの定理が成り立つことを示しなさい。 なお、 ピックの定理とは次のようなものです。

　「 図形の中に存在する単位格子の交点の合計 」と「 頂点または辺の上に存在する単位格子の交点の合計を２で割ったもの 」　加えて　それから１を引いたもの　が、 ほぼ図形の面積に等しくなっている。


　　　　　

（ 解 答 ）

　 この三角形に含まれる、 または、 辺や頂点上に存在する格子の交点の数は次のようになります。
　　　　　

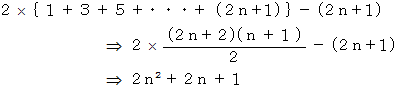
この三角形の辺や頂点上に存在する格子の交点の数は ４ｎ です。

したがって、ピックの定理による三角形の面積は次のようになります。
　　　　　
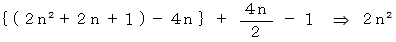
この三角形の面積は公式より次のようになります。
　　　　　
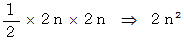
したがって、 両者はピッタリと一致することが解りました。