【 問 題 】

　静止２次元座標系（ X, Y ）の中に移動２次元座標系（ x, y ）があります。X の方向と x の方向は常に同じで、かつ、Y の方向と y の方向は常に同じです。
　移動２次元座標系の原点は静止２次元座標系の原点を中心に原点から距離 5 m だけ離れたところを時計回りに角速度 π/180 rad/s で等速円運動しています。
　移動２次元座標系の中に点Ｐがあり、原点を中心に原点から距離 5 m だけ離れたところを反時計回りに角速度 π/180 rad/s で等速円運動しています。
　ある瞬間に点Ｐは静止２次元座標系（0,10）の位置に存在しました。静止２次元座標系における点Ｐの軌道はどうなっているでしょうか？

　　　　　　　　　　　　　　　　　　　　　　

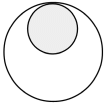
【 解 答 】

　点Ｐが静止２次元座標系（ 0, 10 ）の位置に存在する瞬間から t s 後 の 点Ｐの静止２次元座標系での位置（ P_x, P_y ）は、点Ｐの移動２次元座標系での位置 に 移動２次元座標系の原点の静止２次元座標系での位置を加えて、次のようになります。

　　P_x ＝ 5 cos (tπ/180+π/2) ＋ 5 cos (−tπ/180+π/2)
　　　　＝ −5 sin (tπ/180) − 5 sin (−tπ/180)
　　　　＝ −5 sin (tπ/180) ＋ 5 sin (tπ/180)
　　　　＝ 0

　　P_y ＝ 5 sin (tπ/180+π/2) ＋ 5 sin (−tπ/180+π/2)
　　　　＝ 5 cos (tπ/180) ＋ 5 cos (−tπ/180)
　　　　＝ 10 cos (tπ/180)

したがって、答えは次のようになります。
　　　X ＝ 0　,　−10 ≦ Y ≦ 10