その他の数学 へ戻る【 問 題 】
-
３次元空間に点Ａ ( 1, 1, 1 ) と 点Ｂ ( 1, −1, −1 ) がある。
ベクトルＯＡ と ベクトルＯＢ が張る平行四辺形の面積を求めよ。
-
＊ いろんな解法があると思いますが、比較的簡単な計算ですむ方法を２通り紹介します。
Ａ ＝ ＯＡ Ｂ ＝ ＯＢ 求める平行四辺形の面積を S とする。
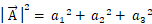
より、S2 ＝ ｜ＯＡ×ＯＢ｜2 ＝ {(−1)−(−1)}2 ＋ {(＋1)−(−1)}2 ＋ {(−1)−(1)}2 ＝→ 8
より、S2 ＝ ( 12＋12＋12 ) × { 12＋(−1)2＋(−1)2 } − { 1×1 ＋ 1×(−1) ＋ 1×(−1) }2 ＝→ 3×3−1 ＝→ 8
したがって、
の式は「２つのベクトルが作る平行四辺形の面積をベクトルの大きさと内積を用いて表す式」であり、導き方を含めて覚えておくといいでしょう。