ｒ ＝ 原点からの距離
　　　θ ＝ z 軸からの傾き
　　　Φ ＝ x 軸からの傾き

　まず、ｒ の値の情報を得ます。そうすると、半径 ｒ の球 のイメージになります。
　次に、θ の値の情報を得ます。そうすると、 x y 平面に平行な 半径 ｒsinθ の円 のイメージになります。
　最後に、 Φ の値の情報を得ます。そうすると、 x y 平面上の x 軸から Φ 傾いた直線 と x y 平面に平行な半径 ｒsinθ の円の x y 平面の投影像 との交点の真上の x y 平面に平行な半径 ｒsinθ の円上の点が、その点になります。そして、その点の座標は次のようになります。
　　　

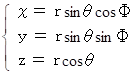
　地球を半径 １ の正球体と仮定し、地球の中心から北極点に向かう方向を z 軸とし、地球の中心から東経０度北緯０度の地点に向かう方向を x 軸とし、地球の中心から東経90度北緯０度の地点に向かう方向を y 軸とします。（ 地球の中心にいて頭が北極を向き右手側にイギリスがあるような姿勢をとっている観察者の座標系にしてみました。）すると、３次元極座標表示から一般の３次元座標表示への座標変数の変換は次のようになります。
　　　

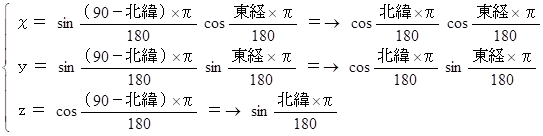
　明石市の真上に静止衛星があるとしたら、その位置は次のようになります。
　　　

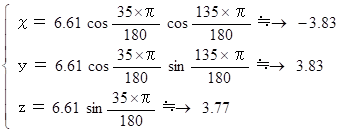
　　　参考 ：　大学生のための物理学 ＞ 天文学 ＞ 静止衛星の軌道は決まっている


３次元極座標表示から一般の３次元座標表示への座標変数の変換 ：

東経（−180 〜＋180 ） 度
北緯（−90 〜＋90 ） 度

　　

x ＝
y ＝
ｚ ＝
x ²＋ y ²＋ｚ² ＝


日本って結構バランスの良い地点にあるんですね。

十進Basic による計算 ：
　　LET z = SQR(1/3)
　　LET b = 90-ACOS(z)*180/PI
　　LET a = (PI/4)*180/PI+90
　　PRINT "東経 ＝";a
　　PRINT "北緯 ＝";b
　　END
　　　　　　　　a ＝ 135
　　　　　　　　b ≒ 35.26439