複素平面での複素数の積分はスカラー場の線積分になります。 ベクトル場の線積分とは異なります。 複素平面上に複素数によるスカラー場が形成されているとします。 その線積分は一般的には曲線に沿って行われますが、 今回は直線に沿って行うことにします。

　 まず、 一様なスカラー場 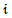が形成されている場合を考えます。 これを次の直線分に沿って線積分してみましょう。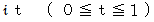
　　　　
ちなみに、 この直線分は虚数軸上の座標値 ０ から １ の間の直線分です。

本題に戻って、求める線積分は次のようになります。
　　　　

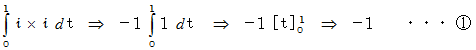
次に、 一様なスカラー場 を次の直線分に沿って線積分してみましょう。
　　　　
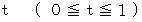
ちなみに、 この直線分は実数軸上の座標値 ０ から １ の間の直線分です。

本題に戻って、 求める線積分は次のようになります。
　　　　

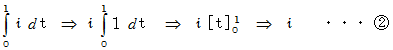
その次に、 一様なスカラー場 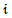を次の直線分に沿って線積分してみましょう。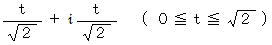
　　　　
　 ちなみに、 この直線分は原点を一端とし、 実数軸とも虚数軸とも４５度の角度で交わります。 また、 この直線分の長さは次のようになります。
　　　　

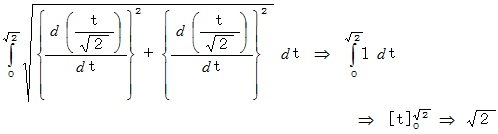
本題に戻って、 求める線積分は次のようになります。
　　　　


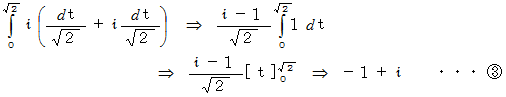
　 さて今度は、 次のような関数 で表されるスカラー場 が形成されている場合を考えます。
　　　　
　 ちなみに、 このスカラー場の値は座標値と同じ値であり、 その大きさは原点からの隔たりを表します。

まず、 虚数軸上の座標値 ０ から １ の間の直線分に沿って線積分してみましょう。
　　　　

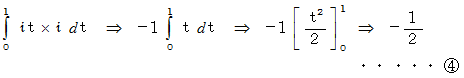
次に、 実数軸上の座標値 ０ から １ の間の直線分に沿って線積分してみましょう。
　　　　

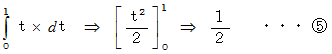
その次に、 さきほどの斜めの長さ 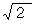の直線分に沿って線積分してみましょう。
　　　　

　 は と とを足した値になっていますが、 は と を足した値にはなっていません。 ということは、 一様なスカラー場という条件でのみ、 線積分するルートが異なっても始点と終点が同じであれば、 線積分の結果が同じになると予想できそうです。


　さて、 今回は複素平面上の複素数によるスカラー場を直線分に沿って線積分しましたが、 閉曲線に沿って線積分すると面白いことになります。 簡単に言いますと、 一般的には になるけれど、 スカラー場が次のような関数で表される場合は原点を含む閉曲線で線積分すると になるということです。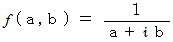
　　　　
　 そうなるイメージを、 長沼伸一郎先生が 「 物理数学の直観的方法 （ BLUE BACKS ）」 の中で紹介しておられますが、 目から鱗です。 ヒントはオイラーの定理と極座標変換ですが、 その前提となる発想が見事で、 このような発想は長沼先生にしかできないものと思います。 一読あれ。