【 問 題 】

　 東に 512 m 移動　→　北に 256 m 移動　→　西に 128 m 移動　→　南に 64 m 移動　→　東に 32 m 移動　→　北に 16 m 移動　→　西に 8 m 移動　→　・ ・ ・ ・　というふうにして移動距離が限りなく 0 m に近づくとき、 出発点からどのような位置になるのか答えなさい。

【 解 答 】

東方向への移動 ：

　　　512　→　−128　→　32　→　−8　→　・ ・ ・ ・
　　　第 ｎ 項の値は　512 × (−1/4) ^n−１　である。
　　　これは、 初項 512、 公比 −1/4 の等比数列である。
　　　したがって、 求めるものは次の式である。
　　　　　　


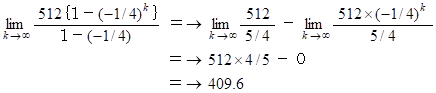
北方向への移動 ：

　　　256　→　−64　→　16　→　−4　→　・ ・ ・ ・
　　　第 ｎ 項の値は　256 × (−1/4) ^n−１　である。
　　　これは、 初項 256、 公比 −1/4 の等比数列である。
　　　したがって、 求めるものは次の式である。
　　　　　





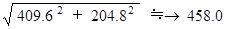
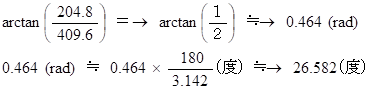
　 したがって、 答えは、 東北東（ 真東から 22.5 度 北方向へ回転した方向 ） よりもやや北よりの方角で、 出発点から約 458 m 離れた所です。