【 問 題 １ 】　　　100！　は、 末桁に ０ がいくつ並ぶか？


【 解 答 】

　　　100以下の自然数で考えます。
　　　　　　５の倍数は　５　10　15　20　・ ・ ・ ・　95　100　の２０個
　　　　　　２５の倍数は　25　50　75　100　の４個

　　　100！　を素因数分解すると
　　　　　　

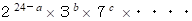　　　　は、素因数に 5 が入っていないため、一の位は ０ ではありません。
　　　したがって、 100！　は、 末桁に ０ が 24 個 並びます。



【 問 題 ２ 】　　　100！　は、 ２進数にすると末桁に ０ がいくつ並ぶか？


【 解 答 】

　　　[ 100/2 ] ＋ [ 100/4 ] ＋ [ 100/8 ] ＋ [ 100/16 ] ＋ [ 100/32 ] ＋ [ 100/64 ]
　　　　　　　　　＝→　50 + 25 + 12 + 6 + 3 + 1　＝→　97
　　　　　　　　　　　　　　　　　＊ [ 100/32 ] ＝ 100/32 を超えない最大の整数
　　　したがって、 10進法では、
　　　　　　100！　＝　２⁹⁷ × ３^a × ５²⁴ × ７^b × ・ ・ ・ ・

　　　２進法では、３^a × ５²⁴ × ７^b × ・ ・ ・ の素因数はすべて１桁目の数字が 1 だから、３^a × ５²⁴ × ７^b × ・ ・ ・ は１桁目の数字は 1 になります。
　　　よって、 ２進数にすると末桁に ０ が 97 個 並びます。