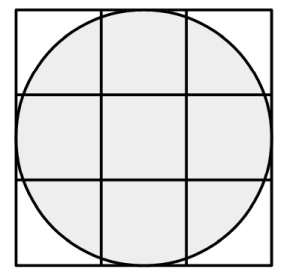
一辺が２ｍの正方形を９分割します。
一辺が２ｍの正方形の内接円を描き、その内部を着色します。
分割された上から２段目左から２番目の正方形を見ると１００％着色されています。
上から １ 段目左から２番目の正方形はどれくらいの割合で着色されていますか？
上から １ 段目左から １ 番目の正方形はどれくらいの割合で着色されていますか？

上記の質問に答えるため、 次のプログラムを作りました。

　 ＜ 解説 ＞

　 まず、 上から２段目の着色された部分の面積を求めます。 それは、 ４つの合同な扇形と４つの合同な直角三角形のタイルが敷き詰められたものですから、 扇形の面積と直角三角形の面積を求めれば分かります。（ ２つの合同な扇形と２つの合同な二等辺三角形のタイルが敷き詰められていると考えてもかまいません。）
　 上から２段目の着色された部分の面積から、 上から２段目左から２段目の着色された部分の面積を引いて２で割れば、 上から １ 段目左から２段目の着色された部分の面積が分かります。

　 次に、 上から １ 段目の着色された部分の面積を求めます。 それは、 着色された円全体の面積から上から２段目の着色された部分の面積を引いて、 ２で割れば分かります。
　 上から １ 段目の着色された部分の面積から、 上から １ 段目左から２段目の着色された部分の面積を引いて２で割れば、 上から １ 段目左から １ 段目の部分の面積が分かります。