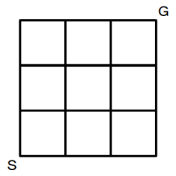
上図の線分は道路だと思ってください。そして線分の交点は街だと思ってください。
　Ｓ街からＧ街までマンハッタン距離にして６ですが、隣り合う街どうしをつなぐ道は渋滞があったりして所要時間がバラバラです。ただし、その所要時間は、時刻によって変化しないものとします。
　Ｓ街からＧ街まで最短時間で移動するにはどのルートを選べばいいでしょうか？　次の例で考えて見ましょう。
　　　　　
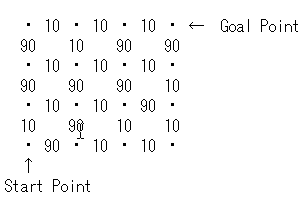
　上図の点は各街を表し、数字は隣り合う街どうしをつなぐ道の所要時間（分）を表しています。
　答えは簡単、ちょうど２時間です。隣り合う街どうしをつなぐ道の所要時間が10分の道ばかりを選んでいけばいいのです。
　今の例は簡単でしたが、一般的にはどのようなアルゴリズムで考えていけばいいでしょう。
　　１．　スタート地点の街からすべての隣の街までの所要時間を調べて街の名前と所要時間を記録する。
　　２．　新しく記録された全ての街について、すべての隣の街までのスタート時点からの所要時間を調べる。
　　３．　今までに記録されていない街については、その名とスタート時点からの所要時間を記録する。
　　４．　今までに記録されている街については、スタート時点からの所要時間が短くなった場合のみ記録する。
　　５．　２〜４を繰り返す。

　では、上図について具体的にやってみましょう。

(0,0)=0 :　(0,1)=10　(1,0)=90
　　　　記入は　(0,1)=10　(1,0)=90
(0,1)=10 :　(0,2)=100　(0,0)=20　(1,1)=20
　　　　記入は　(0,2)=100　(1,1)=20
(1,0)=90 :　(1,1)=180　(2,0)=100　(0,0)=180
　　　　記入は　(2,0)=100
(0,2)=100 :　(0,3)=190　(0,1)=190　(1,2)=110
　　　　記入は　(0,3)=190　(1,2)=110
(1,1)=20 :　(1,2)=110　(1,0)=110　(2,1)=30　(0,1)=30
　　　　記入は　(2,1)=30
(2,0)=100 :　(2,1)=110　(3,0)=110　(1,0)=110
　　　　記入は　(3,0)=110
(0,3)=190 :　(0,2)=280　(1,3)=200
　　　　記入は　(1,3)=200
(1,2)=110 :　(1,3)=120　(1,1)=200　(2,2)=120　(0,2)=120
　　　　記入は　(1,3)=120　(2,2)=120
(2,1)=30 :　(2,2)=120　(2,0)=40　(3,1)=120　(1,1)=40
　　　　記入は　(2,0)=40　(3,1)=120
(3,0)=110 :　(3,1)=120　(2,0)=120
　　　　記入は　なし
以下（略）

　隣どうしの移動所要時間を 10 〜 99 秒のうちから無作為に選んでから、 移動最短時間を求めるプログラムを作ってみました。

　





プログラムの内容 ：