論理学 へ戻る【 問 題 】
-
１問１点の10問で10点満点の○×式試験がある。
第１問から第５問まではＡ君とＢ君の答えは同じ○であった。
第６問から第10問までは２人の答えはすべて異なっていた。
Ａ君は８点、Ｂ君は７点であった。
第１問から第５問まで、○が正解なのは何問あるか？
-
Ａ君が正解した問題の集合をＡとし、Ｂ君が正解した問題の集合をＢとする。
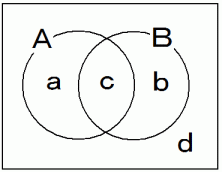
第１問から第５問は Ａ ∩ Ｂ または Ａ ∩ Ｂ の要素である。
第６問から第10問は Ａ ∩ Ｂ または Ａ ∩ Ｂ の要素である。
Ａの要素の数は８個である。
Ｂの要素の数は７個である。
Ａ ∩ Ｂ または Ａ ∩ Ｂ の要素の数は５個である。
Ａ ∩ Ｂ または Ａ ∩ Ｂ の要素の数は５個である。
Ａ ∩ Ｂ の要素の数は最大５個であり、Ａの要素の数は８個より、Ａ ∩ Ｂ の要素の数は３個以上でなければならない。
よって、 Ａ ∩ Ｂ の要素の数は２個以下でなければならない。
Ａ ∩ Ｂ の要素の数が１または２個であると仮定する。
すると、Ａ ∩ Ｂ の要素の数は３または４個になり、かつ、Ａ ∪ Ｂ の要素の数は８または９個になる。
Ａ ∩ Ｂ の要素の数は最大５個であり、Ａの要素の数は８個より、Ａ ∩ Ｂ の要素の数は３個以上でなければならない。
すると、Ａの要素の数は８個より、Ａ ∩ Ｂ の要素の数は４個以上になる。
したがって、Ａ ∩ Ｂ の要素の数は１個以下になる。
したがって、Ｂの要素の数は５個以下になる。
これはＢの要素の数が７個であることと矛盾する。
したがって、Ａ ∩ Ｂ の要素の数は０個であることが分かった。
よって、 Ａ ∩ Ｂ の要素の数は５個である。
というわけで、答えは ５問 である。